Below is a list of most of my papers published in science journals.
You can also find them on my page at Google Scholar, which also provides citation metrics.
I have also co-authored a book about random searches (see here), and co-edited a book about statistical physics and complex systems (see here).
I am a supporter of open access (OA) publishing. Meanwhile, since most of my papers are not in open access journals, as an author or co-author of academic articles I retain the right to e-mail and share copies for educational and academic purposes to collaborators etc. This is a common practice. So, for educational and academic purposes only, you are free to download the PDF files below (but please note that this material is copyrighted). Click on the title of the paper to access the PDF file.
[Updated: July 2023]
Title: Information parity increases on functional brain networks under influence of a psychedelic substance
Author(s): Viol, A (Viol, Aline); Viswanathan, GM (Viswanathan, Gandhimohan M.); Soldatkina, O (Soldatkina, Oleksandra); Palhano-Fontes, F (Palhano-Fontes, Fernanda); Onias, H (Onias, Heloisa); de Araujo, D (de Araujo, Draulio); Hovel, P (Hoevel, Philipp)
Source: JOURNAL OF PHYSICS-COMPLEXITY Volume: 4 Issue: 1 Article Number: 01LT02 DOI: 10.1088/2632-072X/acc22b Published: MAR 1 2023
Abstract: The physical basis of consciousness is one of the most intriguing open questions that contemporary science aims to solve. By approaching the brain as an interactive information system, complex network theory has greatly contributed to understand brain process in different states of mind. We study a non-ordinary state of mind by comparing resting-state functional brain networks of individuals in two different conditions: before and after the ingestion of the psychedelic brew Ayahuasca. In order to quantify the functional, statistical symmetries between brain region connectivity, we calculate the pairwise information parity of the functional brain networks. Unlike the usual approach to quantitative network analysis that considers only local or global scales, information parity instead quantifies pairwise statistical similarities over the entire network structure. We find an increase in the average information parity on brain networks of individuals under psychedelic influences. Notably, the information parity between regions from the limbic system and frontal cortex is consistently higher for all the individuals while under the psychedelic influence. These findings suggest that the resemblance of statistical influences between pair of brain regions activities tends to increase under Ayahuasca effects. This could be interpreted as a mechanism to maintain the network functional resilience.
Title: Threshold-free estimation of entropy from a Pearson matrix
Author(s): Felippe, H (Felippe, H.); Viol, A (Viol, A.); De Araujo, DB (De Araujo, D. B.); Da Luz, MGE (Da Luz, M. G. E.); Palhano-Fontes, F (Palhano-Fontes, F.); Onias, H (Onias, H.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.)
Source: EPL Volume: 141 Issue: 3 Article Number: 31003 DOI: 10.1209/0295-5075/acb5bd Published: FEB 2023
Abstract: There is demand in diverse fields for a reliable method of estimating the entropy associated with correlations. The estimation of a unique entropy directly from the Pearson correlation matrix has remained an open problem for more than half a century. All existing approaches lack generality insofar as they require thresholding choices that arbitrarily remove possibly important information. Here we propose an objective procedure for directly estimating a unique entropy of a general Pearson matrix. We show that upon rescaling the Pearson matrix satisfies all necessary conditions for an analog of the von Neumann entropy to be well defined. No thresholding is required. We demonstrate the method by estimating the entropy from neuroimaging time series of the human brain under the influence of a psychedelic.
Title: Speedup of the Metropolis protocol via algorithmic optimization
Author(s): Macias-Medri, AE (Macias-Medri, A. E.); Viswanathan, GM (Viswanathan, G. M.); Fiore, CE (Fiore, C. E.); Koehler, M (Koehler, M.); da Luz, MGE (da Luz, M. G. E.)
Source: JOURNAL OF COMPUTATIONAL SCIENCE Volume: 66 Article Number: 101910 DOI: 10.1016/j.jocs.2022.101910 Early Access Date: NOV 2022 Published: JAN 2023
Abstract: The Metropolis algorithm is widely used in Monte Carlo (MC) simulations in diverse areas of science and technology, especially for problems formulated in terms of lattice models. A common situation is the necessity to perform long sequential processing, e.g., when looking for equilibrium states of distinct physical systems. Hence, even marginal increases in efficiency of the algorithm individual steps can lead to significant reductions in absolute execution runtimes. Usual speedup procedures include hardware updates, parallelization (when possible) and sampling methods. Here we follow a different direction in trying to decrease the full execution times of MC approaches: algorithmic optimization. We show that the algorithms can be improved by implementing relatively few and simple changes in their organization and structure. First, we discuss some refinements for the pseudo-random number generator, addressing the broadly employed Mersenne-Twister algorithm (MT19937-64). Second, we develop a protocol to precalculate the Boltzmann factor, thereby avoiding the high cost of repeatedly calls to this exponential function (indeed, a very recurring step in the standard Metropolis method). To benchmark our proposals we choose the Ising model since it is one of the best known and more extensively studied problems in statistical physics. We consider the mentioned optimizations and different computational elements, like compilers and Hamiltonian variables ranges, testing the efficiency to obtain the system solutions. Our results suggest that the present set of improvement schemes-namely; decreasing the processing time for both, to generate a random number and to implement the one-flip Metropolis step; systematically enforcing optimization for the maximum quantity of algorithm structures accessing random numbers in a code; and considerably reducing the amount of required computations of the MC probabilistic actualization term-might constitute a relevant addition to the existing collection of expediting techniques in MC computational routines.
Author(s): Carames, LGP (Carames, L. G. P.); Matos, YB (Matos, Y. B.); Bartumeus, F (Bartumeus, F.); Bezerra, CG (Bezerra, C. G.); Macri, T (Macri, T.); da Luz, MGE (da Luz, M. G. E.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICAL REVIEW E Volume: 106 Issue: 5 Article Number: 054147 DOI: 10.1103/PhysRevE.106.054147 Published: NOV 22 2022
Abstract: The Levy flight foraging hypothesis states that organisms must have evolved adaptations to exploit Levy walk search strategies. Indeed, it is widely accepted that inverse square Levy walks optimize the search efficiency in foraging with unrestricted revisits (also known as nondestructive foraging). However, a mathematically rigorous demonstration of this for dimensions D 2 is still lacking. Here we study the very closely related problem of a Levy walker inside annuli or spherical shells with absorbing boundaries. In the limit that corresponds to the foraging with unrestricted revisits, we show that inverse square Levy walks optimize the search. This constitutes the strongest formal result to date supporting the optimality of inverse square Levy walks search strategies.
Title: What Does It Take to Solve the 3D Ising Model? Minimal Necessary Conditions for a Valid Solution
Author(s): Viswanathan, GM (Viswanathan, Gandhimohan M.); Portillo, MAG (Portillo, Marco Aurelio G.); Raposo, EP (Raposo, Ernesto P.); da Luz, MGE (da Luz, Marcos G. E.)
Source: ENTROPY Volume: 24 Issue: 11 Article Number: 1665 DOI: 10.3390/e24111665 Published: NOV 2022
Abstract: An exact solution of the Ising model on the simple cubic lattice is one of the long-standing open problems in rigorous statistical mechanics. Indeed, it is generally believed that settling it would constitute a methodological breakthrough, fomenting great prospects for further application, similarly to what happened when Lars Onsager solved the two-dimensional model eighty years ago. Hence, there have been many attempts to find analytic expressions for the exact partition function Z, but all such attempts have failed due to unavoidable conceptual or mathematical obstructions. Given the importance of this simple yet paradigmatic model, here we set out clear-cut criteria for any claimed exact expression for Z to be minimally plausible. Specifically, we present six necessary-but not sufficient-conditions that Z must satisfy. These criteria will allow very quick plausibility checks of future claims. As illustrative examples, we discuss previous mistaken “solutions”, unveiling their shortcomings.
Title: Effect of the search space dimensionality for finding close and faraway targets in random searches
Author(s): Colaco, JR (Colaco, J. R.); Araujo, HA (Araujo, H. A.); da Luz, MGE (da Luz, M. G. E.); Viswanathan, GM (Viswanathan, G. M.); Bartumeus, F (Bartumeus, F.); Raposo, EP (Raposo, E. P.)
Source: PHYSICAL REVIEW E Volume: 106 Issue: 3 Article Number: 034124 DOI: 10.1103/PhysRevE.106.034124 Published: SEP 15 2022
Abstract: investigate the dependence on the search space dimension of statistical properties of random searches with Levy alpha-stable and power-law distributions of step lengths. We find that the probabilities to return to the last target found (P-0) and to encounter faraway targets (P-L), as well as the associated Shannon entropy S, behave as a function of a quite differently in one (1D) and two (2D) dimensions, a somewhat surprising result not reported until now. While in 1D one always has P-0 >= P-L, an interesting crossover takes place in 2D that separates the search regimes with P-0 > P-L for higher alpha and P-0 < P-L for lower alpha, depending on the initial distance to the last target found. We also obtain in 2D a maximum in the entropy S for alpha is an element of(0, 2], not observed in 1D apart from the trivial alpha -> 0 ballistic limit. Improving the understanding of the role of dimensionality in random searches is relevant in diverse contexts, as in the problem of encounter rates in biology and ecology.
Title: A random walk model with a mixed memory profile: Exponential and rectangular profile
Author(s): de Lacerda, KJCC (de Lacerda, K. J. C. C.); da Silva, LR (da Silva, L. R.); Viswanathan, GM (Viswanathan, G. M.); Cressoni, JC (Cressoni, J. C.); da Silva, MAA (da Silva, M. A. A.)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 597 Article Number: 127301 DOI: 10.1016/j.physa.2022.127301 Early Access Date: APR 2022 Published: JUL 1 2022
Abstract: The theory of Markovian random walks is consolidated and very well understood, however the theory of non-Markovian random walks presents many challenges due to its remarkably rich phenomenology. An important open problem in this context is to study how the diffusive properties of random walk processes change when memory induced correlations are introduced. In this work we propose a model of a random walk that evolves in time according to past memories selected from rectangular (flat) and exponentially decaying memory profiles. In this mixed memory profile model, the walker remembers either the last B steps with equal a priori probability or the steps A prior to B with exponentially decaying probability, for a total number of steps equal to A + B. The diffusive behavior of the walk is numerically examined through the Hurst exponent (H). Even in the lack of exact solutions, we are still able to show that the model can be mapped onto a RW model with rectangular memory profile. (c) 2022 Elsevier B.V. All rights reserved.
Author(s): Viswanathan, GM (Viswanathan, G. M.)
Source: INTERNATIONAL JOURNAL OF MODERN PHYSICS B Volume: 36 Issue: 07N08 Article Number: 2240010 DOI: 10.1142/S0217979222400100 Published: MAR 20 2022
Abstract: A challenging problem in physics concerns the possibility of forecasting rare but extreme phenomena such as large earthquakes, financial market crashes and material rupture. A promising line of research involves the early detection of precursory log-periodic oscillations to help forecast extreme events in collective phenomena where discrete scale invariance plays an important role. Here we investigate two distinct approaches towards the general problem of how to detect log-periodic oscillations in arbitrary time series without prior knowledge of the location of the moveable singularity. We first show that the problem has a definite solution in Fourier space; however, the technique involved requires an unrealistically large signal-to-noise ratio. Then we show that the quadrature signal obtained via analytic continuation onto the imaginary axis, using the Hilbert transform, necessarily retains the log-periodicities found in the original signal. This finding allows the development of a new method of detecting log-periodic oscillations that relies on calculation of the instantaneous phase of the analytic signal. We then illustrate the method by applying it to the stock market crash of 1987 and explore the important role played by positive feedback mechanisms in relation to economic bubble formation, financial crashes, log-periodic dynamics and analytic behavior. Finally, we discuss the relevance of these findings for parametric rather than nonparametric estimation of critical times.
Author(s): Dossetti, V (Dossetti, V); Viswanathan, GM (Viswanathan, G. M.); Kenkre, VM (Kenkre, V. M.)
Source: JOURNAL OF STATISTICAL MECHANICS-THEORY AND EXPERIMENT Volume: 2022 Issue: 3 Article Number: 033210 DOI: 10.1088/1742-5468/ac59b8 Published: MAR 1 2022
Abstract: We present numerical investigations into the question of the validity of the Boltzmann prescription in statistical mechanics for large systems, addressing the issue of whether extensivity of energy implies the extensivity of the Boltzmann entropy. The importance of the question stems from the fact that it is currently considered open by some investigators but quite settled by others. We report ab initio results for gas-like Hamiltonian systems with long-range as well as short-range interactions, based on simulations that explicitly consider more than 2(30) approximate to 10(9) states of the full Hilbert space. The basis of the technique is Monte Carlo algorithms. Despite the largeness of the numbers used, careful inspection shows that the systems studied are still too small to settle uniquely the issues raised. Therefore, the new approach outlined represents a first step in addressing on first principles the question of non-extensive statistical mechanics. General theoretical comments are also supplied to supplement the numerical investigations.
Title: Spectrum of the tight-binding model on Cayley trees and comparison with Bethe lattices
Author(s): Ostilli, M (Ostilli, M.); Bezerra, CG (Bezerra, Claudionor G.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICAL REVIEW E Volume: 105 Issue: 3 Article Number: 034123 DOI: 10.1103/PhysRevE.105.034123 Published: MAR 17 2022
Abstract: There are few exactly solvable lattice models and even fewer solvable quantum lattice models. Here we address the problem of finding the spectrum of the tight-binding model (equivalently, the spectrum of the adjacency matrix) on Cayley trees. Recent approaches to the problem have relied on the similarity between the Cayley tree and the Bethe lattice. Here, we avoid to make any ansatz related to the Bethe lattice due to fundamental differences between the two lattices that persist even when taking the thermodynamic limit. Instead, we show that one can use a recursive procedure that starts from the boundary and then use the canonical basis to derive the complete spectrum of the tight-binding model on Cayley trees. Our resulting algorithm is extremely efficient, as witnessed with remarkable large trees having hundreds of shells. We also show that, in the thermodynamic limit, the density of states is dramatically different from that of the Bethe lattice.
Author(s): Nicolau, NS (Nicolau, N. S.); Araujo, HA (Araujo, H. A.); Viswanathan, GM (Viswanathan, G. M.); da Luz, MGE (da Luz, M. G. E.); Raposo, EP (Raposo, E. P.)
Source: JOURNAL OF PHYSICS A-MATHEMATICAL AND THEORETICAL Volume: 54 Issue: 32 Article Number: 325006 DOI: 10.1088/1751-8121/ac0f17 Published: AUG 13 2021
Abstract: We have extended the Fock space (FS) approach to address the relevant problem of evaluating the mean first passage time (MFPT) and absorption probabilities of a Levy random particle in a discrete finite interval with absorbing boundaries. In this approach the master equation is cast in the form of a real-valued Schrodinger-like equation with a Hamiltonian-like operator related to the transition probabilities, defined by the Levy jump lengths. We present a comprehensive study of such quantities as a function of the eigenvalues and eigenvectors of the quasi-Hamiltonian, Levy stability index alpha, and the particle’s starting position. The predicted asymptotic behavior of the absorption probabilities is finely captured under the FS approach. Moreover, by considering as well the continuous space limit, our findings nicely match the exact analytical result for a Levy flier in continuous bounded space. For comparison, we also provide Monte Carlo results with good agreement with the FS calculations. The MFPT and absorption probabilities are relevant in a number of practical contexts, such as animal foraging and light transmission in randomly scattering media, and our findings may be useful to advance the understanding of these systems.
Title: The double hypergeometric series for the partition function of the 2D anisotropic Ising model
Author(s): Viswanathan, GM (Viswanathan, G. M.)
Source: JOURNAL OF STATISTICAL MECHANICS-THEORY AND EXPERIMENT Volume: 2021 Issue: 7 Article Number: 073104 DOI: 10.1088/1742-5468/ac0f71 Published: JUL 2021
Abstract: In 1944 Lars Onsager published the exact partition function of the ferromagnetic Ising model on the infinite square lattice in terms of a definite integral. Only in the literature of the last decade, however, has it been recast in terms of special functions. Until now all known formulas for the partition function in terms of special functions have been restricted to the important special case of the isotropic Ising model with symmetric couplings. Indeed, the anisotropic model is more challenging because there are two couplings and hence two reduced temperatures, one for each of the two axes of the square lattice. Hence, standard special functions of one variable are inadequate to the task. Here, we reformulate the partition function of the anisotropic Ising model in terms of the Kampe de Feriet function, which is a double hypergeometric function in two variables that is more general than the Appell hypergeometric functions. Finally, we present hypergeometric formulas for the generating function of multipolygons of given length on the infinite square lattice, for isotropic as well as anisotropic edge weights. For the isotropic case, the results allow easy calculation, to arbitrary order, of the celebrated series found by Cyril Domb.
Title: Landscape-scaled strategies can outperform Levy random searches
Author(s): Ferreira, J (Ferreira, J.); Raposo, EP (Raposo, E. P.); Araujo, HA (Araujo, H. A.); Luz, MGE (Luz, M. G. E.); Viswanathan, GM (Viswanathan, G. M.); Bartumeus, F (Bartumeus, F.); Campos, D (Campos, D.)
Source: PHYSICAL REVIEW E Volume: 103 Issue: 2 Article Number: 022105 DOI: 10.1103/PhysRevE.103.022105 Published: FEB 4 2021
Abstract: Information on the relevant global scales of the search space, even if partial, should conceivably enhance the performance of random searches. Here we show numerically and analytically that the paradigmatic uninformed optimal Levy searches can be outperformed by informed multiple-scale random searches in one (1D) and two (2D) dimensions, even when the knowledge about the relevant landscape scales is incomplete. We show in the low-density nondestructive regime that the optimal efficiency of biexponential searches that incorporate all key scales of the 1D landscape of size L decays asymptotically as eta(opt) similar to 1/root L overcoming the result eta(opt) similar to 1/root Lln L) of optimal Levy searches. We further characterize the level of limited information the searcher can have on these scales. We obtain the phase diagram of bi- and triexponential searches in 1D and 2D. Remarkably, even for a certain degree of lack of information, partially informed searches can still outperform optimal Levy searches. We discuss our results in connection with the foraging problem.
Title: Comment on “Inverse Square Levy Walks are not Optimal Search Strategies for d >= 2”
Author(s): Buldyrev, SV (Buldyrev, S. V.); Raposo, EP (Raposo, E. P.); Bartumeus, F (Bartumeus, F.); Havlin, S (Havlin, S.); Rusch, FR (Rusch, F. R.); da Luz, MGE (da Luz, M. G. E.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICAL REVIEW LETTERS Volume: 126 Issue: 4 Article Number: 048901 DOI: 10.1103/PhysRevLett.126.048901 Published: JAN 28 2021
Author(s): A. Viol, H. Felippe Jr., Fernanda Palhano-Fontes, Heloisa Onias, Draulio B. de Araujo, G. M. Viswanathan
Source: Revista Brasileira de Ensino de Fı́sica Volume: 43 Article Number e20200440 DOI: 10.1590/1806-9126-RBEF-2020-0440 Published: 2021
Abstract: The primary aim of statistical mechanics is to relate the micropscopic physics governed by Newton’s laws, or else by quantum mechanics, to the macroscopic physics governed by the laws of thermodynamics. Macroscopic properties, such as temperature, may have no meaning at the microscopic level, but they arise as emergent properties in statistical mechanics when the number of particles becomes sufficiently large. The success of statistical mechanics in explaining and predicting a variety of macroscopic phenomena has motivated the application of concepts and methods of statistical physics to study complex systems and complex networks, including in neuroscience. Our aim here is to apply this approach to a key problem in neuroscience: how can we quantitatively understand the neural correlates of altered mental states induced by psychedelic substances? We first give an overview of basic concepts concerning functional connectivity of brain regions. We then discuss the phenomenology and the neuroscience related to psychedelics. Finally, we review some studies that have applied statistical physics and the theory of complex networks to try to gain a better understanding of the brain under the influence of psychedelics.
Title: Scale-free behavior in hailstone sequences generated by the Collatz map
Author(s): da Luz, MGE (da Luz, M. G. E.); dos Santos, DMG (dos Santos, D. M. G.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICAL REVIEW RESEARCH Volume: 3 Issue: 1 Article Number: 013073 DOI: 10.1103/PhysRevResearch.3.013073 Published: JAN 22 2021
Abstract: The Collatz conjecture, perhaps the most elementary unsolved problem in mathematics, claims that for all positive integers n, the map n bar right arrow n/2 (n even) and n bar right arrow 3n + 1 (n odd) reaches 1 after a finite number of iterations. We examine the Collatz map’s orbits, known as hailstone sequences, to determine whether or not they exhibit scale-invariant behavior, in analogy with certain processes observed in real physical systems. We develop an efficient way to generate orbits for extremely large n (e.g., higher than n similar to 10(3000)), allowing us to statistically analyze very long sequences. We find strong evidence of a scale-free power law for the Collatz map. We analytically derive the scaling exponents, displaying excellent agreement with the numerical estimations. The scale-free sequences seen in the Collatz dynamics are consistent with geometric Brownian motion with drift, which is compatible with the validity of the Collatz conjecture. Our results lead to another conjecture (conceivably testable through direct, nonetheless very time consuming, numerical simulations): Given an initial n, the average number of iterations needed to reach 1 is proportional, to lowest order, to log[n] (basis 10).
Author(s): Almeida, LA (Almeida, L. A.); Pereira, ES (Pereira, E. S.); Borges, GM (Borges, G. M.); Damineli, A (Damineli, A.); Michtchenko, TA (Michtchenko, T. A.); Viswanathan, GM (Viswanathan, G. M.)
Source: MONTHLY NOTICES OF THE ROYAL ASTRONOMICAL SOCIETY Volume: 497 Issue: 3 Pages: 4022-4029 DOI: 10.1093/mnras/staa2185 Published: SEP 2020
Abstract: Eclipse timing variation analysis has become a powerful method to discover planets around binary systems. We applied this technique to investigate the eclipse times of GK Vir. This system is a post-common envelope binary with an orbital period of 8.26 h. Here, we present 10 new eclipse times obtained between 2013 and 2020. We calculated the O-C diagram using a linear ephemeris and verified a clear orbital period variation (OPV) with a cyclic behaviour. We investigated if this variation could be explained by the Applegate mechanism, the apsidal motion, or the light travel time (LTT) effect. We found that the Applegate mechanism would hardly explain the OPV with its current theoretical description. We obtained using different approaches that the apsidal motion is a less likely explanation than the LTT effect. We showed that the LTT effect with one circumbinary body is the most likely cause for the OPV, which was reinforced by the orbital stability of the third body. The LTT best solution provided an orbital period of similar to 24 yr for the outer body. Under the assumption of coplanarity between the external body and the inner binary, we obtained a Jupiter-like planet around the GK Vir. In this scenario, the planet has one of the longest orbital periods, with a full observational baseline, discovered so far. However, as the observational baseline of GK Vir is smaller than twice the period found in the O-C diagram, the LTT solution must be taken as preliminary.
Title: The physics of stochastic processes applied to binary options in financial markets
Author(s): J.S. LIMA, T.C. ABDIAS, I. M. MIRANDA and G. M. VISWANATHAN
Source: REVISTA BRASILEIRA DE ENSINO DE FISICA Volume: 42 Article Number: e20200002 Published: 2020
Abstract: The analogy between the problem of a player who bets money iteratively in a game of chance and a random walker in one dimension with an absorbing boundary is well known. These and other connections between finance and physics motivated the emergence of the field of econophysics in the 1990s. Since the subject matter is still not well known at the level of undergraduate physics programs, here we first review some basic concepts, such as martingales, financial derivatives and stock options. Our objectives are the following: (i) to explain how binary options work; (ii) to simulate stochastically the behavior of the balance sheet curve for different hit rates; (iii) to run tests of the success rates for the stochastic oscillator indicator in financial time series of historical data. This indicator is widely used by binary option traders, so it is an ideal illustrative example. Our results show that it is difficult to obtain consistent profits, even using strategies based on martingales or “Soros” leveraging to recover previous losses. The empirical characterization of this difficulty may help to make clearer the unpredictability and high degree of complexity of the behavior seen in financial markets.
Title: Revisiting Levy flights on bounded domains: a Fock space approach
Author(s): Araujo, HA (Araujo, H. A.); Lukin, MO (Lukin, M. O.); da Luz, MGE (da Luz, M. G. E.); Viswanathan, GM (Viswanathan, G. M.); Santos, FAN (Santos, F. A. N.); Raposo, EP (Raposo, E. P.)
Source: JOURNAL OF STATISTICAL MECHANICS-THEORY AND EXPERIMENT Volume: 2020 Issue: 8 Article Number: 083202 DOI: 10.1088/1742-5468/aba593 Published: AUG 2020
Abstract: The statistical description of a one-dimensional superdiffusive Levy flier restricted to a finite domain is well known to be technically involving. For example, in this type of process the probability distributionP(x,t) and survival probabilityS(t) cannot be obtained from the method of images. Other methods, such as the fractional derivative approach, also find technical difficulties due to the long jumps combined with the presence of absorbing boundaries. Here we revisit this problem through a different point of view. We map the corresponding master equation to a Schrodinger-like equation and then describe the Levy flier evolution in a Fock space. The system states are assigned to the available positions in the discrete space. The Hamiltonian-like matrix is calculated for any Levy index alpha is an element of (0, 2]. For the system sizes studied here the computation of its eigenvalues and eigenvectors are performed using a symbolic computing software. This method allows to build the time evolution operator, the distributionP(x,t) and the survival probabilityS(t). We compare our results forP(x,t) with direct Monte Carlo simulations and find a good agreement for all alpha is an element of (0, 2]. Similarly, our results forS(t) nicely agree with the numerical simulations for any timet, including the short-term behavior. In the long-term asymptotic limit we identify the crossover between the power-law and exponential behaviors, which emerge respectively when only one or both boundaries are reached by the Levy flier. Comparisons with some exact expressions for Levy flights in the continuous space limit also display good agreement. We conclude our analysis by discussing the possibility of extending the present framework to general bounded random walks and flights.
Author(s): Rusch, F (Rusch, F.); Wosniack, ME (Wosniack, M. E.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.); Luz, MGE (Luz, M. G. E.)
Source: PHYSICAL REVIEW E Volume: 102 Issue: 1 Article Number: 012126 DOI: 10.1103/PhysRevE.102.012126 Published: JUL 13 2020
Abstract: Transient regimes, often difficult to characterize, can be fundamental in establishing final steady states features of reaction-diffusion phenomena. This is particularly true in ecological problems. Here, through both numerical simulations and an analytic approximation, we analyze the transient of a nonequilibrium superdiffusive random search when the targets are created at a certain rate and annihilated upon encounters (a key dynamics, e.g., in biological foraging). The steady state is achieved when the number of targets stabilizes to a constant value. Our results unveil how key features of the steady state are closely associated to the particularities of the initial evolution. The searching efficiency variation in time is also obtained. It presents a rather surprising universal behavior at the asymptotic limit. These analyses shed some light into the general relevance of transients in reaction-diffusion systems.
Author(s): de Lacerda, KJCC (de Lacerda, K. J. C. C.); Cressoni, JC (Cressoni, J. C.); Viswanathan, GM (Viswanathan, G. M.); da Silva, MAA (da Silva, M. A. A.)
Source: EPL Volume: 130 Issue: 2 DOI: 10.1209/0295-5075/130/20004 Published: APR 2020
Abstract: The exactly solvable Elephant Random Walk (ERW) model introduced by Schutz and Trimper 15 years ago stimulated research that led to many new insights and advances in understanding anomalous diffusion. Such models have two distinct ingredients: i) long-range -possibly complete- memory of the past behavior and ii) a decision-making rule that makes use of the memory. These models are memory-neutral: the decision-making rule does not distinguish between short-term (or recent) memories and long-term (or old) memories. Here we relax the condition of memory neutrality, so that memory and decision-making become interconnected. We investigate the diffusive properties of random walks that evolve according to memory-biased decision processes and find remarkably rich phase diagrams, including a phase of log-periodic superdiffusion that may be associated with old memory and negative feedback regulating mechanisms. Our results overturn the conventional wisdom concerning the origin of log-periodicity in non-Markovian models. All previously known non-Markovian random walk models that exhibit log-periodicities in their behavior have incomplete (or damaged) memory of their history. Here we show that log-periodicity can appear even if the memory is complete, so long as there is a memory bias.
Title: A Langevin dynamics approach to the distribution of animal move lengths
Author(s): Santana, JV (Santana-Filho, J. V.); Raposo, EP (Raposo, E. P.); Macedo, AMS (Macedo, A. M. S.); Vasconcelos, GL (Vasconcelos, G. L.); Viswanathan, GM (Viswanathan, G. M.); Bartumeus, F (Bartumeus, F.); da Luz, MGE (da Luz, M. G. E.)
Source: JOURNAL OF STATISTICAL MECHANICS-THEORY AND EXPERIMENT Volume: 2020 Issue: 2 Article Number: 023406 DOI: 10.1088/1742-5468/ab6ddf Published: FEB 2020
Abstract: Movement is fundamental to the animal ecology, determining how, when, and where an individual interacts with the environment. The animal dynamics is usually inferred from trajectory data described as a combination of moves and turns, which are generally influenced by the vast range of complex stochastic stimuli received by the individual as it moves. Here we consider a statistical physics approach to study the probability distribution of animal move lengths based on stochastic differential Langevin equations and the superstatistics formalism. We address the stochastic influence on the move lengths as a Wiener process. Two main cases are considered: one in which the statistical properties of the noise do not change along the animal’s path and another with heterogeneous noise statistics. The latter is treated in a compounding statistics framework and may be related to heterogeneous landscapes. We study Langevin dynamics processes with different types of nonlinearity in the deterministic component of movement and both linear and nonlinear multiplicative stochastic processes. The move length distributions derived here comprise the possibility of movement multiscales, diffusive and superdiffusive (Levy-like) dynamics, and include most of the distributions currently considered in the literature of animal movement, as well as some new proposals.
Author(s): da Silva, MAA (da Silva, M. A. A.); Rocha, EC (Rocha, E. C.); Cressoni, JC (Cressoni, J. C.); da Silva, LR (da Silva, L. R.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 538 Article Number: 122793 DOI: 10.1016/j.physa.2019.122793 Published: JAN 15 2020
Abstract: One of the most important quantities of interest in the theory of diffusion and transport is the random walk propagator. For Markovian processes, such as the standard Brownian random walk and Levy flights, the functional form of the random walk propagator is well understood. Similarly, for certain kinds of simple non-Markovian processes, such as Levy walks, the problem can be mapped to a solvable Markovian model. However, more complicated non-Markovian walks pose a challenge. Here we study a non-Markovian model that is rich enough to exhibit superdiffusion, normal diffusion and subdiffusion regimes (Kumar, Harbola, and Lindenberg (2010)). We numerically estimate propagators for this model and obtain good fits with a family of non-Levy propagators based on the Tsallis q-exponential function. We conclude that stops and restrictions play similar roles in the long time limit of the propagator. (C) 2019 Elsevier B.V. All rights reserved.
Title: Why Levy alpha-stable distributions lack general closed-form expressions for arbitrary alpha
Author(s): Rocha, EC (Rocha, E. C.); da Luz, MGE (da Luz, M. G. E.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICAL REVIEW E Volume: 100 Issue: 1 Article Number: 010103 DOI: 10.1103/PhysRevE.100.010103 Published: JUL 22 2019
Abstract: The ubiquitous Levy alpha-stable distributions lack general closed-form expressions in terms of elementary functions-Gaussian and Cauchy cases being notable exceptions. To better understand this 80-year-old conundrum, we study the complex analytic continuation p(alpha)(z), z is an element of C, of the symmetric Levy alpha-stable distribution family p(alpha)(x), x is an element of R, parametrized by 0 < alpha <= 2. We first extend known but obscure results, and give a new proof that p(alpha)(z) is holomorphic on the entire complex plane for 1 < alpha <= 2, whereas p(alpha)(z) is not even meromorphic on C for 0 < alpha < 1. Next, we unveil the complete complex analytic structure of p(alpha)(z) using domain coloring. Finally, motivated by these insights, we argue that there cannot be closed-form expressions in terms of elementary functions for p(alpha)(x) for general alpha.
Author(s): Viol, A (Viol, Aline); Palhano-Fontes, F (Palhano-Fontes, Fernanda); Onias, H (Onias, Heloisa); de Araujo, DB (de Araujo, Draulio B.); Hovel, P (Hoevel, Philipp); Viswanathan, GM (Viswanathan, Gandhi M.)
Source: ENTROPY Volume: 21 Issue: 2 Article Number: 128 DOI: 10.3390/e21020128 Published: FEB 2019
Abstract: With the aim of further advancing the understanding of the human brain’s functional connectivity, we propose a network metric which we term the geodesic entropy. This metric quantifies the Shannon entropy of the distance distribution to a specific node from all other nodes. It allows to characterize the influence exerted on a specific node considering statistics of the overall network structure. The measurement and characterization of this structural information has the potential to greatly improve our understanding of sustained activity and other emergent behaviors in networks. We apply this method to study how the psychedelic infusion Ayahuasca affects the functional connectivity of the human brain in resting state. We show that the geodesic entropy is able to differentiate functional networks of the human brain associated with two different states of consciousness in the awaking resting state: (i) the ordinary state and (ii) a state altered by ingestion of the Ayahuasca. The functional brain networks from subjects in the altered state have, on average, a larger geodesic entropy compared to the ordinary state. Finally, we discuss why the geodesic entropy may bring even further valuable insights into the study of the human brain and other empirical networks.
Title: Identifying dynamical structures in the physical space of stochastic processes
Author(s): Wosniack, ME (Wosniack, M. E.); Santos, MC (Santos, M. C.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.); da Luz, MGE (da Luz, M. G. E.); Schulman, LS (Schulman, L. S.)
Source: EPL Volume: 125 Issue: 2 Article Number: 20004 DOI: 10.1209/0295-5075/125/20004 Published: JAN 2019
Abstract: Characterizing dynamical patterns in the (physical) state space of stochastic processes can be a challenging task. From two visualization techniques, the observable-representation and k-means clustering, a unified framework to identify such structures is developed. The only information required is the system transition matrix R (a quantity that can be directly accessed from experimental data). The approach is illustrated through the analysis of random searches for targets distributed in patchy environments. The protocol-for R constructed from a typical tracked long trajectory-is able to reveal the shape and locations of all the landscape patches. The method constitutes a valuable new tool to study the underlying geometry of general stochastic processes.
Title: Log-periodicity in piecewise ballistic superdiffusion: Exact results
Author(s): Cressoni, JC (Cressoni, J. C.); Viswanathan, GM (Viswanathan, G. M.); da Silva, MAA (da Silva, M. A. A.)
Source: PHYSICAL REVIEW E Volume: 98 Issue: 5 Article Number: 052102 DOI: 10.1103/PhysRevE.98.052102 Published: NOV 1 2018
Abstract: Small log-periodic oscillations have been observed in many systems and have previously been studied via renormalization-group approaches in the context of critical phenomena [Gluzman and Sornette, Phys. Rev. E 65, 036142 (2002); Derrida and Giacomin, J. Stat. Phys. 154, 286 (2014)]. Here we report their appearance in a random walk model with damaged memory, and we develop an exact discrete-time solution, free from adjustable parameters. Our results shed light on log-periodicity and how it arises. We also discuss continuous-time approaches to the solution along with their limitations and advantages. We show that, as a direct consequence of memory damage, the first moment for the model acquires piecewise ballistic behavior. The piecewise segments are separated by regularly placed singular points. Log-periodicity in this model is seen to be due to memory damage. Remarkably, piecewise ballistic behavior is only observed if one uses the discrete-time solution, because the continuous-time solution does not correctly account for the model’s discrete-time dynamics.
Title: An efficient series approximation for the Levy alpha-stable symmetric distribution
Author(s): Crisanto-Neto, JC (Crisanto-Neto, J. C.); da Luz, MGE (da Luz, M. G. E.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICS LETTERS A Volume: 382 Issue: 35 Pages: 2408-2413 DOI: 10.1016/j.physleta.2018.07.013 Published: SEP 7 2018
Abstract: A relevant problem in the statistical and mathematical physics literature is to derive numerically accurate expressions to calculate Levy alpha-stable distributions P-alpha(x; beta). On the formal side, important exact results rely on special functions, such as Meijer-G, Fox-H and finite sums of hypergeometric functions, with only a few exceptional cases expressed in terms of elementary functions. Hence, from a more practical point of view, methods such as series expansions are in order, e.g., to allow for the estimation of the Levy distribution with high numerical precision, even though most of the existing approaches are restricted to a subset of the distribution parameters and/or usually demand relatively time-consuming sophisticated algorithms. Here we present a rather simple truncated expansion for the case of symmetric Levy distributions P-alpha(x) (beta = 0). This is achieved by dividing the full range of integration into windows, performing proper series expansion inside each, and then calculating the integrals term by term. The obtained representation is convergent for any 0 <= alpha <= 2. Moreover, its accuracy is directly controlled by the number of terms in the truncated expression, being straightforward to implement numerically. As we show with different examples, for almost all allowable alpha’s the calculations lead to P-alpha(x) with reasonable low absolute error for computationally inexpensive simulations.
Title: Surname complex network for Brazil and Portugal
Author(s): Ferreira, GD (Ferreira, G. D.); Viswanathan, GM (Viswanathan, G. M.); da Silva, LR (da Silva, L. R.); Herrmann, HJ (Herrmann, H. J.)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 499 Pages: 198-207 DOI: 10.1016/j.physa.2018.02.008 Published: JUN 1 2018
Abstract: We present a study of social networks based on the analysis of Brazilian and Portuguese family names (surnames). We construct networks whose nodes are names of families and whose edges represent parental relations between two families. From these networks we extract the connectivity distribution, clustering coefficient, shortest path and centrality. We find that the connectivity distribution follows an approximate power law. We associate the number of hubs, centrality and entropy to the degree of miscegenation in the societies in both countries. Our results show that Portuguese society has a higher miscegenation degree than Brazilian society. All networks analyzed lead to approximate inverse square power laws in the degree distribution. We conclude that the thermodynamic limit is reached for small networks (3 or 4 thousand nodes). The assortative mixing of all networks is negative, showing that the more connected vertices are connected to vertices with lower connectivity. Finally, the network of surnames presents some small world characteristics.
Title: Lambda CDM model with dissipative nonextensive viscous dark matter
Author(s): Gimenes, HS (Gimenes, H. S.); Viswanathan, GM (Viswanathan, G. M.); Silva, R (Silva, R.)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 494 Pages: 331-339 DOI: 10.1016/j.physa.2017.12.064 Published: MAR 15 2018
Abstract: Many models in cosmology typically assume the standard bulk viscosity. We study an alternative interpretation for the origin of the bulk viscosity. Using nonadditive statistics proposed by Tsallis, we propose a bulk viscosity component that can only exist by a nonextensive effect through the nonextensive/dissipative correspondence (NexDC). In this paper, we consider a ACDM model for a flat universe with a dissipative nonextensive viscous dark matter component, following the Eckart theory of bulk viscosity, without any perturbative approach. In order to analyze cosmological constraints, we use one of the most recent observations of Type la Supernova, baryon acoustic oscillations and cosmic microwave background data.
Title: The evolutionary origins of Levy walk foraging
Author(s): Wosniack, ME (Wosniack, Marina E.); Santos, MC (Santos, Marcos C.); Raposo, EP (Raposo, Ernesto P.); Viswanathan, GM (Viswanathan, Gandhi M.); da Luz, MGE (da Luz, Marcos G. E.)
Source: PLOS COMPUTATIONAL BIOLOGY Volume: 13 Issue: 10 Article Number: e1005774 DOI: 10.1371/journal.pcbi.1005774 Published: OCT 2017
Abstract: We study through a reaction-diffusion algorithm the influence of landscape diversity on the efficiency of search dynamics. Remarkably, the identical optimal search strategy arises in a wide variety of environments, provided the target density is sparse and the searcher’s information is restricted to its close vicinity. Our results strongly impact the current debate on the emergentist vs. evolutionary origins of animal foraging. The inherent character of the optimal solution (i.e., independent on the landscape for the broad scenarios assumed here) suggests an interpretation favoring the evolutionary view, as originally implied by the Levy flight foraging hypothesis. The latter states that, under conditions of scarcity of information and sparse resources, some organisms must have evolved to exploit optimal strategies characterized by heavy-tailed truncated power-law distributions of move lengths. These results strongly suggest that Levy strategies-and hence the selection pressure for the relevant adaptations-are robust with respect to large changes in habitat. In contrast, the usual emergentist explanation seems not able to explain how very similar Levy walks can emerge from all the distinct non-Levy foraging strategies that are needed for the observed large variety of specific environments. We also report that deviations from Levy can take place in plentiful ecosystems, where locomotion truncation is very frequent due to high encounter rates. So, in this case normal diffusion strategies-performing as effectively as the optimal one-can naturally emerge from Levy. Our results constitute the strongest theoretical evidence to date supporting the evolutionary origins of experimentally observed Levy walks.
Author(s): Viol, A (Viol, A.); Palhano-Fontes, F (Palhano-Fontes, Fernanda); Onias, H (Onias, Heloisa); de Araujo, DB (de Araujo, Draulio B.); Viswanathan, GM (Viswanathan, G. M.)
Source: SCIENTIFIC REPORTS Volume: 7 Article Number: 7388 DOI: 10.1038/s41598-017-06854-0 Published: AUG 7 2017
Abstract: The entropic brain hypothesis holds that the key facts concerning psychedelics are partially explained in terms of increased entropy of the brain’s functional connectivity. Ayahuasca is a psychedelic beverage of Amazonian indigenous origin with legal status in Brazil in religious and scientific settings. In this context, we use tools and concepts from the theory of complex networks to analyze resting state fMRI data of the brains of human subjects under two distinct conditions: (i) under ordinary waking state and (ii) in an altered state of consciousness induced by ingestion of Ayahuasca. We report an increase in the Shannon entropy of the degree distribution of the networks subsequent to Ayahuasca ingestion. We also find increased local and decreased global network integration. Our results are broadly consistent with the entropic brain hypothesis. Finally, we discuss our findings in the context of descriptions of “mind-expansion” frequently seen in self-reports of users of psychedelic drugs.
Title: Correspondence between spanning trees and the Ising model on a square lattice
Author(s): Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICAL REVIEW E Volume: 95 Issue: 6 Article Number: 062138 DOI: 10.1103/PhysRevE.95.062138 Published: JUN 30 2017
Abstract: An important problem in statistical physics concerns the fascinating connections between partition functions of lattice models studied in equilibrium statistical mechanics on the one hand and graph theoretical enumeration problems on the other hand. We investigate the nature of the relationship between the number of spanning trees and the partition function of the Ising model on the square lattice. The spanning tree generating function T (z) gives the spanning tree constant when evaluated at z = 1, while giving the lattice green function when differentiated. It is known that for the infinite square lattice the partition function Z(K) of the Ising model evaluated at the critical temperature K = K-c is related to T (1). Here we show that this idea in fact generalizes to all real temperatures. We prove that [Z(K) sech 2K](2) = k exp [T (k)], where k = 2 tanh(2K) sech(2K). The identical Mahler measure connects the two seemingly disparate quantities T (z) and Z(K). In turn, the Mahler measure is determined by the random walk structure function. Finally, we show that the the above correspondence does not generalize in a straightforward manner to nonplanar lattices.
Author(s): Crisanto-Neto, JC (Crisanto-Neto, J. C.); da Luz, MGE (da Luz, M. G. E.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.)
Source: JOURNAL OF PHYSICS A-MATHEMATICAL AND THEORETICAL Volume: 49 Issue: 37 Article Number: 375001 DOI: 10.1088/1751-8113/49/37/375001 Published: SEP 16 2016
Abstract: In practice, the Levy alpha-stable distribution is usually expressed in terms of the Fourier integral of its characteristic function. Indeed, known closed form expressions are relatively scarce given the huge parameters space: 0 < alpha <= 2 (Levy index), -1 <= beta <= 1 (skewness), sigma > 0 (scale), and -infinity < mu < infinity (shift). Hence, systematic efforts have been made towards the development of proper methods for analytically solving the mentioned integral. As a further contribution in this direction, here we propose a new way to tackle the problem. We consider an approach in which one first solves the Fourier integral through a formal (thus not necessarily convergent) series representation. Then, one uses (if necessary) a pertinent sum-regularization procedure to the resulting divergent series, so as to obtain an exact formula for the distribution, which is amenable to direct numerical calculations. As a concrete study, we address the centered, symmetric, unshifted and unscaled distribution (beta = 0, mu = 0, sigma = 1), with alpha= alpha(M) = 2 M, M = 1, 2, 3… Conceivably, the present protocol could be applied to other sets of parameter values.
Title: Subjective expectation of rewards can change the behavior of smart but impatient foragers
Author(s): da Luz, MGE (Eleuterio da Luz, Marcos Gomes); Raposo, EP (Raposo, Ernesto P.); Viswanathan, GM (Viswanathan, Gandhimohan M.)
Source: PROCEEDINGS OF THE NATIONAL ACADEMY OF SCIENCES OF THE UNITED STATES OF AMERICA Volume: 113 Issue: 31 Pages: 8571-8573 DOI: 10.1073/pnas.1609369113 Published: AUG 2 2016
By: Moura, TRS (Moura, Thiago R. S.); Viswanathan, GM (Viswanathan,
G. M.); da Silva, MAA (da Silva, M. A. A.); Cressoni, JC (Cressoni,
J. C.); da Silva, LR (da Silva, L. R.)
Title: Transient superdiffusion in random walks with a q-exponentially decaying memory profile
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 453 Pages: 259-263 DOI: 10.1016/j.physa.2016.02.005 Published: JUL 1 2016
Abstract: We propose a random walk model with q-exponentially decaying
memory profile. The q-exponential function is a generalization of the
ordinary exponential function. In the limit q -> 1, the q-exponential
becomes the ordinary exponential function. This model presents a
Markovian diffusive regime that is characterized by finite memory
correlations. It is well known, that central limit theorems prohibit
superdiffusion for Markovian walks with finite variance of step
sizes. In this problem we report the outcome of a transient
superdiffusion for finite sized walks. (C) 2016 Elsevier B.V. All
rights reserved.
By: Azevedo, DL (Azevedo, D. L.); da Silva, KAT (da Silva, Kleber
A. T.); Mauriz, PW (Mauriz, P. W.); Viswanathan, GM (Viswanathan,
G. M.); Oliveira, FA (Oliveira, F. A.)
Title: Fractal behavior of poly(GC) and poly(TA) DNA segments arranged in quasiperiodic Fibonacci sequence
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 445 Pages: 27-34 DOI: 10.1016/j.physa.2015.08.029 Published: MAR 1 2016
Abstract: We used the atomistic molecular mechanics method with a
well-known universal force field (UFF), as implemented in FORCITE
module, to investigate the fractal properties of the poly GC and poly
TA base pairs diluted in solvent, grown in conformity with the
quasiperiodic Fibonacci sequence. It was obtained through simulations,
and demonstrated that solvent-accessible surface area and volume of
these molecules follow power-law behavior that depends on the chain
length with exponent near 1 for the volume, and for the surface. The
exponents calculated presented a dependence on the solvent probe
radius. It was demonstrated that only in a rigid simple model these
exponents converge to unity as the chain length increases to
infinity. However the reason for fractionary exponents found here
could be just attributed to finite size effect, but in fact, the
flexibility plays a central rule in a real molecular system, and could
explain the fractionary exponents obtained here. Both classes of
macromolecules analyzed present a self-similar characteristic that
could assist for understanding of several biological properties, and
result in a variety of potential applications. (C) 2015 Elsevier
B.V. All rights reserved.
By: Wosniack, ME (Wosniack, M. E.); Raposo, EP (Raposo, E. P.);
Viswanathan, GM (Viswanathan, G. M.); da Luz, MGE (da Luz, M. G. E.)
Title: Efficient search of multiple types of targets
Source: PHYSICAL REVIEW E Volume: 92 Issue: 6 Article Number: 062135
DOI: 10.1103/PhysRevE.92.062135 Published: DEC 21 2015
Abstract: Random searches often take place in fragmented
landscapes. Also, in many instances like animal foraging, significant
benefits to the searcher arise from visits to a large diversity of
patches with a well-balanced distribution of targets found. Up to
date, such aspects have been widely ignored in the usual
single-objective analysis of search efficiency, in which one seeks to
maximize just the number of targets found per distance traversed. Here
we address the problem of determining the best strategies for the
random search when these multiple-objective factors play a key role in
the process. We consider a figure of merit (efficiency function),
which properly “scores” the mentioned tasks. By considering random
walk searchers with a power-law asymptotic Levy distribution of step
lengths, p(l) similar to l(-mu), with 1 < mu <= 3, we show that the
standard optimal strategy with mu(opt) approximate to 2 no longer
holds universally. Instead, optimal searches with enhanced
superdiffusivity emerge, including values as low as mu(opt)
approximate to 1.3 (i.e., tending to the ballistic limit). For the
general theory of random search optimization, our findings emphasize
the necessity to correctly characterize the multitude of aims in any
concrete metric to compare among possible candidates to efficient
strategies. In the context of animal foraging, our results might
explain some empirical data pointing to stronger superdiffusion (mu <
2) in the search behavior of different animal species, conceivably
associated to multiple goals to be achieved in fragmented landscapes.
By: Wosniack, ME (Wosniack, M. E.); Raposo, EP (Raposo, E. P.);
Viswanathan, GM (Viswanathan, G. M.); da Luz, MGE (da Luz, M. G. E.)
Title: A parallel algorithm for random searches
Source: COMPUTER PHYSICS COMMUNICATIONS Volume: 196 Pages: 390-397
DOI: 10.1016/j.cpc.2015.07.014 Published: NOV 2015
Abstract: We discuss a parallelization procedure for a two-dimensional
random search of a single individual, a typical sequential process. To
assure the same features of the sequential random search in the
parallel version, we analyze the former spatial patterns of the
encountered targets for different search strategies and densities of
homogeneously distributed targets. We identify a lognormal tendency
for the distribution of distances between consecutively detected
targets. Then, by assigning the distinct mean and standard deviation
of this distribution for each corresponding configuration in the
parallel simulations (constituted by parallel random walkers), we are
able to recover important statistical properties, e.g., the target
detection efficiency, of the original problem. The proposed parallel
approach presents a speedup of nearly one order of magnitude compared
with the sequential implementation. This algorithm can be easily
adapted to different instances, as searches in three dimensions. Its
possible range of applicability covers problems in areas as diverse as
automated computer searchers in high-capacity databases and animal
foraging. (C) 2015 Elsevier B.V. All rights reserved.
By: da Luz, MGE (da Luz, M. G. E.); Raposo, EP (Raposo, E. P.);
Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICS OF LIFE REVIEWS Volume: 14 Pages: 94-98 DOI:
10.1016/j.plrev.2015.07.007
By: Vieira, TM (Vieira, Tiago M.); Viswanathan, GM (Viswanathan,
Gandhi M.); da Silva, LR (da Silva, Luciano R.)
Title: Information entropy of classical versus explosive percolation
Source: EUROPEAN PHYSICAL JOURNAL B Volume: 88 Issue: 9 Article
Number: 213 DOI: 10.1140/epjb/e2015-60500-0 Published: SEP 2015
Abstract: We study the Shannon entropy of the cluster size
distribution in classical as well as explosive percolation, in order
to estimate the uncertainty in the sizes of randomly chosen
clusters. At the critical point the cluster size distribution is a
power-law, i.e. there are clusters of all sizes, so one expects the
information entropy to attain a maximum. As expected, our results show
that the entropy attains a maximum at this point for classical
percolation. Surprisingly, for explosive percolation the maximum
entropy does not match the critical point. Moreover, we show that it
is possible to determine the critical point without using the
conventional order parameter, just analysing the entropy’s
derivatives.
By: Tromer, RM (Tromer, R. M.); Barbosa, MB (Barbosa, M. B.);
Bartumeus, F (Bartumeus, F.); Catalan, J (Catalan, J.); da Luz, MGE
(da Luz, M. G. E.); Raposo, EP (Raposo, E. P.); Viswanathan, GM
(Viswanathan, G. M.) Author Identifiers: Author ResearcherID Number
ORCID Number Catalan, Jordi A-5420-2008 0000-0002-2934-4013
Title: Inferring Levy walks from curved trajectories: A rescaling method
Source: PHYSICAL REVIEW E Volume: 92 Issue: 2 Article Number: 022147
DOI: 10.1103/PhysRevE.92.022147 Published: AUG 28 2015
Abstract: An important problem in the study of anomalous diffusion and
transport concerns the proper analysis of trajectory data. The
analysis and inference of Levy walk patterns from empirical or
simulated trajectories of particles in two and three-dimensional
spaces (2D and 3D) is much more difficult than in 1D because path
curvature is nonexistent in 1D but quite common in higher
dimensions. Recently, a new method for detecting Levy walks, which
considers 1D projections of 2D or 3D trajectory data, has been
proposed by Humphries et al. The key new idea is to exploit the fact
that the 1D projection of a high-dimensional Levy walk is itself a
Levy walk. Here, we ask whether or not this projection method is
powerful enough to cleanly distinguish 2D Levy walk with added
curvature from a simple Markovian correlated random walk. We study the
especially challenging case in which both 2D walks have exactly
identical probability density functions (pdf) of step sizes as well as
of turning angles between successive steps. Our approach extends the
original projection method by introducing a rescaling of the projected
data. Upon projection and coarse-graining, the renormalized pdf for
the travel distances between successive turnings is seen to possess a
fat tail when there is an underlying Levy process. We exploit this
effect to infer a Levy walk process in the original high-dimensional
curved trajectory. In contrast, no fat tail appears when a (Markovian)
correlated random walk is analyzed in this way. We show that this
procedure works extremely well in clearly identifying a Levy walk even
when there is noise from curvature. The present protocol may be useful
in realistic contexts involving ongoing debates on the presence (or
not) of Levy walks related to animal movement on land (2D) and in air
and oceans (3D).
By: Bento, EP (Bento, E. P.); Viswanathan, GM (Viswanathan, G. M.); da
Luz, MGE (da Luz, M. G. E.); Silva, R (Silva, R.)
Title: Reply to “Comment on ‘Third law of thermodynamics as a key test of generalized entropies’ “
Source: PHYSICAL REVIEW E Volume: 92 Issue: 1 Article Number: 016104
DOI: 10.1103/PhysRevE.92.016104 Published: JUL 14 2015
Abstract: In Bento et al. [Phys. Rev. E 91, 039901 (2015)] we develop
a method to verify if an arbitrary generalized statistics does or does
not obey the third law of thermodynamics. As examples, we address two
important formulations, Kaniadakis and Tsallis. In their Comment on
the paper, Bagci and Oikonomou suggest that our examination of the
Tsallis statistics is valid only for q >= 1, using arguments like
there is no distribution maximizing the Tsallis entropy for the
interval q < 0 (in which the third law is not verified) compatible
with the problem energy expression. In this Reply, we first (and most
importantly) show that the Comment misses the point. In our original
work we have considered the now already standard construction of the
Tsallis statistics. So, if indeed such statistics lacks a maximization
principle (a fact irrelevant in our protocol), this is an inherent
feature of the statistics itself and not a problem with our
analysis. Second, some arguments used by Bagci and Oikonomou (for 0 <
q < 1) reflect a misunderstanding of our explicit calculations. These
arguments are then clarified under our approach and illustrated
through a simple two-level system.
By: Niebuhr, BBS (Niebuhr, Bernardo B. S.); Wosniack, ME (Wosniack,
Marina E.); Santos, MC (Santos, Marcos C.); Raposo, EP (Raposo,
Ernesto P.); Viswanathan, GM (Viswanathan, Gandhimohan M.); da Luz,
MGE (da Luz, Marcos G. E.); Pie, MR (Pie, Marcio R.)
Title: Survival in patchy landscapes: the interplay between dispersal, habitat loss and fragmentation
Source: SCIENTIFIC REPORTS Volume: 5 Article Number: 11898 DOI:
10.1038/srep11898 Published: JUL 7 2015
Abstract: Habitat loss and fragmentation are important factors
determining animal population dynamics and spatial distribution. Such
landscape changes can lead to the deleterious impact of a significant
drop in the number of species, caused by critically reduced survival
rates for organisms. In order to obtain a deeper understanding of the
threeway interplay between habitat loss, fragmentation and survival
rates, we propose here a spatially explicit multi-scaled movement
model of individuals that search for habitat. By considering basic
ecological processes, such as predation, starvation (outside the
habitat area), and competition, together with dispersal movement as a
link among habitat areas, we show that a higher survival rate is
achieved in instances with a lower number of patches of larger
areas. Our results demonstrate how movement may counterbalance the
effects of habitat loss and fragmentation in altered landscapes. In
particular, they have important implications for conservation planning
and ecosystem management, including the design of specific features of
conservation areas in order to enhance landscape connectivity and
population viability.
By: Viswanathan, GM (Viswanathan, G. M.)
Title: The hypergeometric series for the partition function of the 2D Ising model
Source: JOURNAL OF STATISTICAL MECHANICS-THEORY AND EXPERIMENT Article Number: P07004 DOI: 10.1088/1742-5468/2015/07/P07004 Published: JUL 2015
Abstract: In 1944 Onsager published the formula for the partition
function of the Ising model for the infinite square lattice. He was
able to express the internal energy in terms of a special function,
but he left the free energy as a definite integral. Seven decades
later, the partition function and free energy have yet to be written
in closed form, even with the aid of special functions. Here we
evaluate the definite integral explicitly, using hypergeometric
series. Let beta denote the reciprocal temperature, J the coupling and
f the free energy per spin. We prove that -beta f = ln(2 cosh 2K) –
kappa F-2(4)3[(1,) (1,)(2,) (3/2,)(2,) (3/2)(2,); 16 kappa(2)], where
F-p(q) is the generalized hypergeometric function, K = beta J, and 2
kappa = tanh 2K sech 2K.
By: Wosniack, ME (Wosniack, M. E.); Santos, MC (Santos, M. C.);
Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.); da
Luz, MGE (da Luz, M. G. E.)
Title: Robustness of optimal random searches in fragmented environments
Source: PHYSICAL REVIEW E Volume: 91 Issue: 5 Article Number: 052119
DOI: 10.1103/PhysRevE.91.052119 Published: MAY 13 2015
Abstract: The random search problem is a challenging and
interdisciplinary topic of research in statistical physics. Realistic
searches usually take place in nonuniform heterogeneous distributions
of targets, e.g., patchy environments and fragmented habitats in
ecological systems. Here we present a comprehensive numerical study of
search efficiency in arbitrarily fragmented landscapes with unlimited
visits to targets that can only be found within patches. We assume a
random walker selecting uniformly distributed turning angles and step
lengths from an inverse power-law tailed distribution with exponent
mu. Our main finding is that for a large class of fragmented
environments the optimal strategy corresponds approximately to the
same value mu(opt) approximate to 2. Moreover, this exponent is
indistinguishable from the well-known exact optimal value mu(opt) = 2
for the low-density limit of homogeneously distributed revisitable
targets. Surprisingly, the best search strategies do not depend (or
depend only weakly) on the specific details of the
fragmentation. Finally, we discuss the mechanisms behind this observed
robustness and comment on the relevance of our results to both the
random search theory in general, as well as specifically to the
foraging problem in the biological context.
By: Bento, EP (Bento, E. P.); Viswanathan, GM (Viswanathan, G. M.); da
Luz, MGE (da Luz, M. G. E.); Silva, R (Silva, R.)
Title: Third law of thermodynamics as a key test of generalized entropies (vol 91, 022105, 2015)
Source: PHYSICAL REVIEW E Volume: 91 Issue: 3 Article Number: 039901 DOI: 10.1103/PhysRevE.91.039901
Published: MAR 10 2015
By: da Silva, MAA (da Silva, M. A. A.); Viswanathan, GM (Viswanathan,
G. M.); Cressoni, JC (Cressoni, J. C.) Author Identifiers: Author
ResearcherID Number ORCID Number da Silva, Marco H-3614-2012
0000-0002-6720-5073
Title: A two-dimensional non-Markovian random walk leading to anomalous diffusion
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 421 Pages: 522-532 DOI: 10.1016/j.physa.2014.11.047 Published: MAR 1 2015
Abstract: Exact solutions are rare for non-Markovian random walk
models even in 1D, and much more so in 2D. Here we propose a 2D
genuinely non-Markovian random walk model with a very rich phase
diagram, such that the motion in each dimension can belong to one of 3
categories: (i) subdiffusive, (ii) superdiffusive, or (iii) normally
diffusive. The main advance reported here is a different method, and
the consequent physical insight, for analytically solving this
model. Simpler non-Markovian models, such as Levy walks, have been
solved in 2D, but it is not clear if the method of solution could be
made to work for more complicated models such as the one studied
here. We also report the exact solutions for the first two moments of
the random walk propagator, along with the complete phase diagram. The
latter is surprisingly rich and admits diverse diffusion
regimes. Finally we discuss these results in the context of
theoretical underpinnings as well as possible applications. (C) 2014
Elsevier B.V. All rights reserved.
By: Bento, EP (Bento, E. P.); Viswanathan, GM (Viswanathan, G. M.); da
Luz, MGE (da Luz, M. G. E.); Silva, R (Silva, R.)
Title: Third law of thermodynamics as a key test of generalized entropies
Source: PHYSICAL REVIEW E Volume: 91 Issue: 2 Article Number: 022105
DOI: 10.1103/PhysRevE.91.022105 Published: FEB 6 2015
Abstract: The laws of thermodynamics constrain the formulation of
statistical mechanics at the microscopic level. The third law of
thermodynamics states that the entropy must vanish at absolute zero
temperature for systems with nondegenerate ground states in
equilibrium. Conversely, the entropy can vanish only at absolute zero
temperature. Here we ask whether or not generalized entropies satisfy
this fundamental property. We propose a direct analytical procedure to
test if a generalized entropy satisfies the third law, assuming only
very general assumptions for the entropy S and energy U of an
arbitrary N-level classical system. Mathematically, the method relies
on exact calculation of beta = dS/dU in terms of the microstate
probabilities p(i). To illustrate this approach, we present exact
results for the two best known generalizations of statistical
mechanics. Specifically, we study the Kaniadakis entropy S-k,S- which
is additive, and the Tsallis entropy S-q, which is nonadditive. We
show that the Kaniadakis entropy correctly satisfies the third law
only for -1 < k < + 1, thereby shedding light on why. is
conventionally restricted to this interval. Surprisingly, however, the
Tsallis entropy violates the third law for q < 1. Finally, we give a
concrete example of the power of our proposed method by applying it to
a paradigmatic system: the one-dimensional ferromagnetic Ising model
with nearest-neighbor interactions.
By: Bartumeus, F (Bartumeus, Frederic); Raposo, EP (Raposo, Ernesto
P.); Viswanathan, GM (Viswanathan, Gandhimohan M.); da Luz, MGE (da
Luz, Marcos G. E.)
Title: Stochastic Optimal Foraging: Tuning Intensive and Extensive Dynamics in Random Searches
Source: PLOS ONE Volume: 9 Issue: 9 Article Number: e106373 DOI:
10.1371/journal.pone.0106373 Published: SEP 12 2014
Abstract: Recent theoretical developments had laid down the proper
mathematical means to understand how the structural complexity of
search patterns may improve foraging efficiency. Under
information-deprived scenarios and specific landscape configurations,
Levy walks and flights are known to lead to high search
efficiencies. Based on a one-dimensional comparative analysis we show
a mechanism by which, at random, a searcher can optimize the encounter
with close and distant targets. The mechanism consists of combining an
optimal diffusivity (optimally enhanced diffusion) with a minimal
diffusion constant. In such a way the search dynamics adequately
balances the tension between finding close and distant targets, while,
at the same time, shifts the optimal balance towards relatively larger
close-to-distant target encounter ratios. We find that introducing a
multiscale set of reorientations ensures both a thorough local space
exploration without oversampling and a fast spreading dynamics at the
large scale. Levy reorientation patterns account for these properties
but other reorientation strategies providing similar statistical
signatures can mimic or achieve comparable efficiencies. Hence, the
present work unveils general mechanisms underlying efficient random
search, beyond the Levy model. Our results suggest that animals could
tune key statistical movement properties (e.g. enhanced diffusivity,
minimal diffusion constant) to cope with the very general problem of
balancing out intensive and extensive random searching. We believe
that theoretical developments to mechanistically understand stochastic
search strategies, such as the one here proposed, are crucial to
develop an empirically verifiable and comprehensive animal foraging
theory.
By: da Cunha, SD (da Cunha, S. D.); da Silva, LR (da Silva, L. R.);
Viswanathan, GM (Viswanathan, G. M.); Dickman, R (Dickman, Ronald)
Title: Activity, diffusion, and correlations in a two-dimensional conserved stochastic sandpile
Source: JOURNAL OF STATISTICAL MECHANICS-THEORY AND EXPERIMENT Article Number: P08003 DOI: 10.1088/1742-5468/2014/08/P08003 Published: AUG 2014
Abstract: We perform large-scale simulations of a two-dimensional
restricted height conserved stochastic sandpile, focusing on particle
diffusion and mobility, and spatial correlations. Quasistationary (QS)
simulations yield the critical particle density to high precision
[p(c) = 0.7112687(2)], and show that the diffusion constant scales in
the same manner as the activity density, as found previously in the
one-dimensional case. Short-time scaling is characterized by
subdiffusive behavior (mean-square displacement similar to t(gamma)
with gamma < 1), which is easily understood as a consequence of the
initial decay of activity, rho(t) similar to t(-delta), with gamma = 1
– delta. We verify that at criticality, the activity-activity
correlation function C(r) similar to r(-beta/nu perpendicular to), as
expected at an absorbing-state phase transition. Our results for
critical exponents are consistent with, and somewhat more precise
than, predictions derived from the Langevin equation for stochastic
sandpiles in two dimensions.
By: Viswanathan, TM (Viswanathan, T. M.); Viswanathan, GM
(Viswanathan, G. M.)
Source: PHILOSOPHICAL TRANSACTIONS OF THE ROYAL SOCIETY A-MATHEMATICAL PHYSICAL AND ENGINEERING SCIENCES Volume: 372 Issue: 2018 Special Issue: SI Article Number: 20140137 DOI: 10.1098/rsta.2014.0137 Published: JUN 28 2014
By: da Silva, MAA (da Silva, M. A. A.); Viswanathan, GM (Viswanathan,
G. M.); Cressoni, JC (Cressoni, J. C.)
Title: Ultraslow diffusion in an exactly solvable non-Markovian random walk
Source: PHYSICAL REVIEW E Volume: 89 Issue: 5 Article Number: 052110
DOI: 10.1103/PhysRevE.89.052110 Published: MAY 8 2014
Abstract: We study a one-dimensional discrete-time non-Markovian
random walk with strong memory correlations subjected to
pauses. Unlike the Scher-Montroll continuous-time random walk, which
can be made Markovian by defining an operational time equal to the
random-walk step number, the model we study keeps a record of the
entire history of the walk. This new model is closely related to the
one proposed recently by Kumar, Harbola, and Lindenberg [Phys. Rev. E
82, 021101 (2010)], with the difference that in our model the
stochastic dynamics does not stop even in the extreme limit of
subdiffusion. Surprisingly, this small difference leads to large
consequences. The main results we report here are exact results
showing ultraslow diffusion and a stationary diffusion regime (i.e.,
localization). Specifically, the equations of motion are solved
analytically for the first two moments, allowing the determination of
the Hurst exponent. Several anomalous diffusion regimes are apparent,
ranging from superdiffusion to subdiffusion, as well as ultraslow and
stationary regimes. We present the complete phase diffusion diagram,
along with a study of the persistence and the statistics in the
regions of interest.
By: Alves, GA (Alves, G. A.); de Araujo, JM (de Araujo, J. M.);
Cressoni, JC (Cressoni, J. C.); da Silva, LR (da Silva, L. R.); da
Silva, MAA (da Silva, M. A. A.); Viswanathan, GM (Viswanathan, G. M.)
Author Identifiers: Author ResearcherID Number ORCID Number de Araujo,
Joao F-5381-2015 0000-0002-2882-7590 Alves da Silva, Marco Antonio
H-3614-2012 0000-0002-6720-5073
Title: Superdiffusion driven by exponentially decaying memory
Source: JOURNAL OF STATISTICAL MECHANICS-THEORY AND EXPERIMENT Article Number: P01026 DOI: 10.1088/1742-5468/2014/04/P04026 Published: APR 2014
Abstract: A superdiffusive random walk model with exponentially
decaying memory is r(reported. This seems to be a self-contradictory
statement, since it is well known that random walks with exponentially
decaying temporal correlations can be approximated arbitrarily well by
Markov processes and that central limit theorems prohibit,
superdiffusion for Markovian walks with finite variance of step
sizes. The solution to the apparent paradox is that the model is
genuinely non-Markovian, due to a time-dependent decay constant
associated with the exponential behavior.
Title: High frequency energy cascades in inviscid hydrodynamics
Author(s): Costa, ASN (Costa, Adam Smith N.); de Araujo, JM (de Araujo, J. M.); Cohen, N (Cohen, Nir); Lucena, LS (Lucena, Liacir S.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 399 Pages: 137-146 DOI: 10.1016/j.physa.2013.12.019 Published: APR 1 2014
Abstract: With the aim of gaining insight into the notoriously difficult problem of energy and vorticity cascades in high dimensional incompressible flows, we take a simpler and very well understood low dimensional analog and approach it from a new perspective, using the Fourier transform. Specifically, we study, numerically and analytically, how kinetic energy moves from one scale to another in solutions of the hyperbolic or inviscid Burgers equation in one spatial dimension (1D). We restrict our attention to initial conditions which go to zero as x -> +/-infinity. The main result we report here is a Fourier analytic way of describing the cascade process. We find that the cascade proceeds by rapid growth of a crossover scale below which there is asymptotic power law decay of the magnitude of the Fourier transform.
Author(s): Wosniack, ME (Wosniack, M. E.); Santos, MC (Santos, M. C.); Pie, MR (Pie, M. R.); Marques, MCM (Marques, M. C. M.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.); da Luz, MGE (da Luz, M. G. E.)
Source: JOURNAL OF THE ROYAL SOCIETY INTERFACE Volume: 11 Issue: 91 Article Number: 20130887 DOI: 10.1098/rsif.2013.0887 Published: FEB 6 2014
Abstract: Several studies have reported that fragmentation (e.g. of anthropogenic origin) of habitats often leads to a decrease in the number of species in the region. An important mechanism causing this adverse ecological impact is the change in the encounter rates (i.e. the rates at which individuals meet other organisms of the same or different species). Yet, how fragmentation can change encounter rates is poorly understood. To gain insight into the problem, here we ask how landscape fragmentation affects encounter rates when all other relevant variables remain fixed. We present strong numerical evidence that fragmentation decreases search efficiencies thus encounter rates. What is surprising is that it falls even when the global average densities of interacting organisms are held constant. In other words, fragmentation per se can reduce encounter rates. As encounter rates are fundamental for biological interactions, it can explain part of the observed diminishing in animal biodiversity. Neglecting this effect may underestimate the negative outcomes of fragmentation. Partial deforestation and roads that cut through forests, for instance, might be responsible for far greater damage than thought. Preservation policies should take into account this previously overlooked scientific fact.
Title: Bandgap oscillation in quasiperiodic carbon-BN nanoribbons
Author(s): Pedreira, DO (Pedreira, D. O.); Azevedo, S (Azevedo, S.); Bezerra, CG (Bezerra, C. G.); Viol, A (Viol, A.); Viswanathan, GM (Viswanathan, G. M.); Ferreira, MS (Ferreira, M. S.)
Source: SOLID STATE COMMUNICATIONS Volume: 180 Pages: 28-34 DOI: 10.1016/j.ssc.2013.11.023 Published: FEB 2014
Abstract: In this work we address the effects of quasiperiodic disorder on the physical properties of nanoribbons, composed by BN and C, constructed according to the Fibonacci quasiperiodic sequence. We assume BN and C as the building blocks of the resulting quasiperiodic structure. The density of states and energy band gap were obtained through ab-initio calculations based on the density functional theory. We report the effects of the quasiperiodic disorder on the oscillatory behavior of the specific heat, in the low temperature regime, and on the behavior of the energy band gap. In particular, we show that the electronic energy band gap oscillates as a function of the Fibonacci generation index n. Our results suggest that the choice of the building block materials of the quasiperiodic sequence, with appropriate band gap energies, may lead to a tuneable band gap of quasiperiodic nanoribbons. (C) 2013 Elsevier Ltd. All rights reserved.
Title: Exact solution of an anisotropic 2D random walk model with strong memory correlations
Author(s): Cressoni, JC (Cressoni, J. C.); Viswanathan, GM (Viswanathan, G. M.); da Silva, MAA (da Silva, M. A. A.)
Source: JOURNAL OF PHYSICS A-MATHEMATICAL AND THEORETICAL Volume: 46 Issue: 50 Article Number: 505002 DOI: 10.1088/1751-8113/46/50/505002 Published: DEC 20 2013
Abstract: Over the last decade, there has been progress in understanding one-dimensional non-Markovian processes via analytic, sometimes exact, solutions. The extension of these ideas and methods to two and higher dimensions is challenging. We report the first exactly solvable two-dimensional (2D) non-Markovian random walk model belonging to the family of the elephant random walk model. In contrast to Levy walks or fractional Brownian motion, such models incorporate memory effects by keeping an explicit history of the random walk trajectory. We study a memory driven 2D random walk with correlated memory and stops, i.e. pauses in motion. The model has an inherent anisotropy with consequences for its diffusive properties, thereby mixing the dominant regime along one dimension with a subdiffusive walk along a perpendicular dimension. The anomalous diffusion regimes are fully characterized by an exact determination of the Hurst exponent. We discuss the remarkably rich phase diagram, as well as several possible combinations of the independent walks in both directions. The relationship between the exponents of the first and second moments is also unveiled.
Title: Non-Gaussian propagator for elephant random walks
Author(s): da Silva, MAA (da Silva, M. A. A.); Cressoni, JC (Cressoni, J. C.); Schutz, GM (Schuetz, Gunter M.); Viswanathan, GM (Viswanathan, G. M.); Trimper, S (Trimper, Steffen)
Source: PHYSICAL REVIEW E Volume: 88 Issue: 2 Article Number: 022115 DOI: 10.1103/PhysRevE.88.022115 Published: AUG 9 2013
Abstract: For almost a decade the consensus has held that the random walk propagator for the elephant random walk (ERW) model is a Gaussian. Here we present strong numerical evidence that the propagator is, in general, non-Gaussian and, in fact, non-Levy. Motivated by this surprising finding, we seek a second, non-Gaussian solution to the associated Fokker-Planck equation. We prove mathematically, by calculating the skewness, that the ERW Fokker-Planck equation has a non-Gaussian propagator for the superdiffusive regime. Finally, we discuss some unusual aspects of the propagator in the context of higher order terms needed in the Fokker-Planck equation.
Title: Scale-free homophilic network
Author(s): de Almeida, ML (de Almeida, Mauricio L.); Mendes, GA (Mendes, Gabriel A.); Viswanathan, GM (Viswanathan, G. Madras); da Silva, LR (da Silva, Luciano R.)
Source: EUROPEAN PHYSICAL JOURNAL B Volume: 86 Issue: 2 Article Number: 38 DOI: 10.1140/epjb/e2012-30802-x Published: FEB 2013
Abstract: An important aspect governing the growth of complex networks is homophily, which is defined as the tendency of sites to link with others which are similar to themselves. Here, we modify the preferential attachment from Barabasi-Albert model by including a homophilic term. Comparisons are made with the Barabasi-Albert model, fitness model and our present model considering its topological properties: degree distribution, time dependence of the connectivity, shortest path length and clustering coefficient. We verify the existence of a region where the characteristics of sites play an important role in the rate of gaining links as well as in the number of links between sites with similar and dissimilar characteristics.
Title: Dissipative Levy random searches: Universal behavior at low target density
Author(s): Ribeiro-Neto, PJ (Ribeiro-Neto, P. J.); Raposo, EP (Raposo, E. P.); Araujo, HA (Araujo, H. A.); Faustino, CL (Faustino, C. L.); da Luz, MGE (da Luz, M. G. E.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICAL REVIEW E Volume: 86 Issue: 6 Article Number: 061102 DOI: 10.1103/PhysRevE.86.061102 Part: 1 Published: DEC 4 2012
Abstract: We investigate the problem of survival at the very low target-density limit and report on a second-order phase transition for one-dimensional random searches in which the energy cost of locomotion is a function of the distance traveled by the searcher. Surprisingly, from analytical calculations (also tested numerically) we find identical critical exponents for arbitrary energy cost functions. We conclude that there is a single universality class that describes this process.
Title: Robustness of the non-Markovian Alzheimer walk under stochastic perturbation
Author(s): Cressoni, JC (Cressoni, J. C.); da Silva, LR (da Silva, L. R.); Viswanathan, GM (Viswanathan, G. M.); da Silva, MAA (da Silva, M. A. A.)
Source: EPL Volume: 100 Issue: 6 Article Number: 60003 DOI: 10.1209/0295-5075/100/60003 Published: DEC 2012
Abstract: The elephant walk model originally proposed by Schutz and Trimper to investigate non-Markovian processes led to the investigation of a series of other random-walk models. Of these, the best known is the Alzheimer walk model, because it was the first model shown to have amnestically induced persistence-i.e. superdiffusion caused by loss of memory. Here we study the robustness of the Alzheimer walk by adding a memoryless stochastic perturbation. Surprisingly, the solution of the perturbed model can be formally reduced to the solutions of the unperturbed model. Specifically, we give an exact solution of the perturbed model by finding a surjective mapping to the unperturbed model.
Title: Alzheimer random walk model: Two previously overlooked diffusion regimes
Author(s): Cressoni, JC (Cressoni, J. C.); Viswanathan, GM (Viswanathan, G. M.); Ferreira, AS (Ferreira, A. S.); da Silva, MAA (da Silva, M. A. A.)
Source: PHYSICAL REVIEW E volume: 86 Issue: 4 Article Number: 042101 DOI: 10.1103/PhysRevE.86.042101 Part: Part 1 Published: OCT 2 2012
Abstract: A non-Markovian one-dimensional random walk model is studied with emphasis on the phase-diagram, showing all the diffusion regimes, along with the exactly determined critical lines. The model, known as the Alzheimer walk, is endowed with memory-controlled diffusion, responsible for the model’s long-range correlations, and is characterized by a rich variety of diffusive regimes. The importance of this model is that superdiffusion arises due not to memory per se, but rather also due to loss of memory. The recently reported numerically and analytically estimated values for the Hurst exponent are hereby reviewed. We report the finding of two, previously overlooked, phases, namely, evanescent log-periodic diffusion and log-periodic diffusion with escape, both with Hurst exponent H = 1/2. In the former, the log-periodicity gets damped, whereas in the latter the first moment diverges. These phases further enrich the already intricate phase diagram. The results are discussed in the context of phase transitions, aging phenomena, and symmetry breaking.
Title: Conditions under which a superdiffusive random-search strategy is necessary
Author(s): Sotelo-Lopez, SA (Sotelo-Lopez, S. A.); Santos, MC (Santos, M. C.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.); da Luz, MGE (da Luz, M. G. E.)
Source: PHYSICAL REVIEW E Volume: 86 Issue: 3 Article Number: 031133 DOI: 10.1103/PhysRevE.86.031133 Part: Part 1 Published: SEP 24 2012
Abstract: Intuitively, lower target densities and lower detection capabilities should demand more sophisticated search strategies for a random search reasonable outcome. In contrast, when targets are easily found, a simple Brownian random walk strategy is enough. But where is the threshold between these two scenarios and when is optimization really necessary? We address this considering the interplay between two essential scales in random search, the average distance between neighbor targets l(o) and the detection capability r(v). In the limit cases the ratio beta = r(v)/l(o) suffices to characterize the problem. For low (high) beta a superdiffusive behavior is (is not) crucial for the process optimization. However, there is a crossover range, which is a nontrivial function of r(v) and l(o), separating the two regimes. We analyze this intermediate region, common in nature, and discuss the often overlooked important trade between resources availability and the searcher location power. Our results highlight contexts where efficient random search is a key factor for survival, such as in animal foraging.
Title: Superdiffusion in a non-Markovian random walk model with a Gaussian memory profile
Author(s): Borges, GM (Borges, G. M.); Ferreira, AS (Ferreira, A. S.); da Silva, MAA (da Silva, M. A. A.); Cressoni, JC (Cressoni, J. C.); Viswanathan, GM (Viswanathan, G. M.); Mariz, AM (Mariz, A. M.)
Source: EUROPEAN PHYSICAL JOURNAL B Volume: 85 Issue: 9 Article Number: 310 DOI: 10.1140/epjb/e2012-30378-5 Published: SEP 2012
Abstract: Most superdiffusive Non-Markovian random walk models assume that correlations are maintained at all time scales, e. g., fractional Brownian motion, Levy walks, the Elephant walk and Alzheimer walk models. In the latter two models the random walker can always “remember” the initial times near t = 0. Assuming jump size distributions with finite variance, the question naturally arises: is superdiffusion possible if the walker is unable to recall the initial times? We give a conclusive answer to this general question, by studying a non-Markovian model in which the walker’s memory of the past is weighted by a Gaussian centered at time t/2, at which time the walker had one half the present age, and with a standard deviation sigma t which grows linearly as the walker ages. For large widths we find that the model behaves similarly to the Elephant model, but for small widths this Gaussian memory profile model behaves like the Alzheimer walk model. We also report that the phenomenon of amnestically induced persistence, known to occur in the Alzheimer walk model, arises in the Gaussian memory profile model. We conclude that memory of the initial times is not a necessary condition for generating (log-periodic) superdiffusion. We show that the phenomenon of amnestically induced persistence extends to the case of a Gaussian memory profile.
Title: Weakly anomalous diffusion with non-Gaussian propagators
Author(s): Cressoni, JC (Cressoni, J. C.); Viswanathan, GM (Viswanathan, G. M.); Ferreira, AS (Ferreira, A. S.); da Silva, MAA (da Silva, M. A. A.)
Source: PHYSICAL REVIEW E Volume: 86 Issue: 2 Article Number: 022103 DOI: 10.1103/PhysRevE.86.022103 Part: Part 1 Published: AUG 27 2012
Abstract: A poorly understood phenomenon seen in complex systems is diffusion characterized by Hurst exponent H approximate to 1/2 but with non-Gaussian statistics. Motivated by such empirical findings, we report an exact analytical solution for a non-Markovian random walk model that gives rise to weakly anomalous diffusion with H = 1/2 but with a non-Gaussian propagator.
Title: The influence of the environment on Levy random search efficiency: Fractality and memory effects
Author(s): Ferreira, AS (Ferreira, A. S.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.); da Luz, MGE (da Luz, M. G. E.)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 391 Issue: 11 Pages: 3234-3246 DOI: 10.1016/j.physa.2012.01.028 Published: JUN 1 2012
Abstract: An open problem in the field of random searches relates to optimizing the search efficiency in fractal environments. Here we address this issue through a systematic study of Levy searches in landscapes encompassing several degrees of target aggregation and fractality. For scarce resources, non-destructive searches with unrestricted revisits to targets are shown to present universal optimal behavior irrespective of the general scaling properties of the spatial distribution of targets. In contrast, no such universal behavior occurs in the destructive case with forbidden revisits, in which the optimal strategy strongly depends on the degree of target aggregation. We also investigate how the presence of memory and learning skills of the searcher affect the search efficiency. By considering a limiting model in which the searcher learns through recent experience to recognize food-rich areas, we find that a statistical memory of previous encounters does not necessarily increase the rate of target findings in random searches. Instead, there is an optimal extent of memory, dependent on specific details of the search space and stochastic dynamics, which maximizes the search efficiency. This finding suggests a more general result, namely that in some instances there are actual advantages to ignoring certain pieces of partial information while searching for objects. (C) 2012 Elsevier B.V. All rights reserved.
Title: The universality class of random searches in critically scarce environments
Author(s): Faustino, CL (Faustino, C. L.); Lyra, ML (Lyra, M. L.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.); da Luz, MGE (da Luz, M. G. E.)
Source: EPL Volume: 97 Issue: 5 Article Number: 50005 DOI: 10.1209/0295-5075/97/50005 Published: MAR 2012
Abstract: We analyze searchers looking for diffusive targets when the formers rely on the net energy gained from the encounters to maintain the process. The system properties are studied at very low target densities, for the searchers at the edge of extinction. We report that superdiffusion for both types of players confers a substantial increase in the searchers survival rate. A continuous phase transition is observed for any search strategy. From the critical exponents, we find that the problem belongs to the same universality class of directed percolation with absorbing walls. We finally discuss the implications of the random search process criticality to the endurance of searchers as a group and eventual connections with the preservation of biological species. Copyright (C) EPLA, 2012
Title: Levy sections vs. partial sums of heteroscedastic time series
Author(s): Nascimento, CM (Nascimento, C. M.); Helena, ELS (Helena, E. L. S.); Passos, FS (Passos, F. S.); Gleria, I (Gleria, I.); Figueiredo, A (Figueiredo, A.); Viswanathan, GM (Viswanathan, G. M.)
Source: EPL Volume: 96 Issue: 6 Article Number: 68004 DOI: 10.1209/0295-5075/96/68004 Published: DEC 2011
Abstract: Weakly nonstationary processes appear in many challenging problems related to the physics of complex systems. An interesting question is how to quantify the rate of convergence to Gaussian behavior of rescaled heteroscedastic time series with stationary first moments but nonstationary multifractal long-range correlated second moments. Here we use the approach which uses a recently proposed extension of the Levy sections theorem. We analyze statistical and multifractal properties of heteroscedastic time series and find that the Levy sections approach provides a faster convergence to Gaussian behavior relative to the convergence of traditional partial sums of variables. We also observe that the rescaled signals retain multifractal properties even after reaching what appears to be the stable Gaussian regime. Copyright (C) EPLA, 2011
Title: How Landscape Heterogeneity Frames Optimal Diffusivity in Searching Processes
Author(s): Raposo, EP (Raposo, E. P.); Bartumeus, F (Bartumeus, F.); da Luz, MGE (da Luz, M. G. E.); Ribeiro-Neto, PJ (Ribeiro-Neto, P. J.); Souza, TA (Souza, T. A.); Viswanathan, GM (Viswanathan, G. M.)
Source: PLOS COMPUTATIONAL BIOLOGY Volume: 7 Issue: 11 Article Number: e1002233 DOI: 10.1371/journal.pcbi.1002233 Published: NOV 2011
Abstract: Theoretical and empirical investigations of search strategies typically have failed to distinguish the distinct roles played by density versus patchiness of resources. It is well known that motility and diffusivity of organisms often increase in environments with low density of resources, but thus far there has been little progress in understanding the specific role of landscape heterogeneity and disorder on random, non-oriented motility. Here we address the general question of how the landscape heterogeneity affects the efficiency of encounter interactions under global constant density of scarce resources. We unveil the key mechanism coupling the landscape structure with optimal search diffusivity. In particular, our main result leads to an empirically testable prediction: enhanced diffusivity (including superdiffusive searches), with shift in the diffusion exponent, favors the success of target encounters in heterogeneous landscapes.
Author(s): Passos, FS (Passos, F. S.); Nascimento, CM (Nascimento, C. M.); Gleria, I (Gleria, Iram); da Silva, S (da Silva, Sergio); Viswanathan, GM (Viswanathan, G. M.)
Source: EPL Volume: 93 Issue: 5 Article Number: 58006 DOI: 10.1209/0295-5075/93/58006 Published: MAR 2011
Abstract: An important open problem concerns the physical origin of long-range correlations, multifractality and fat-tailed distributions observed in heteroscedastic time series associated with complex systems. Financial stylized facts provides one useful example usually not explained by traditional economic models. We investigate the behavior of an agent-based model consisting of N agents which interact with each other via fixed rules. We show that fat-tailed distributions, long-range correlations, heteroscedasticity and multifractality arise as N becomes large. Our findings suggest that such stylized facts can in principle arise as emergent properties. Copyright (C) EPLA, 2011
Author(s): Viswanathan, TM (Viswanathan, T. M.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHILOSOPHICAL TRANSACTIONS OF THE ROYAL SOCIETY A-MATHEMATICAL PHYSICAL AND ENGINEERING SCIENCES Volume: 369 Issue: 1935 Pages: 359-370 DOI: 10.1098/rsta.2010.0257 Published: JAN 28 2011
Abstract: Strong global solvability is difficult to prove for high-dimensional hydrodynamic systems because of the complex interplay between nonlinearity and scale invariance. We define the Ladyzhenskaya-Lions exponent alpha(L)(n)=(2 + n)/4 for Navier-Stokes equations with dissipation -(-Delta)(alpha) in R(n), for all n >= 2. We review the proof of strong global solvability when alpha >= alpha(L)(n), given smooth initial data. If the corresponding Euler equations for n > 2 were to allow uncontrolled growth of the enstrophy (1/2)parallel to del(u)parallel to(2)(L2), then no globally controlled coercive quantity is currently known to exist that can regularize solutions of the Navier-Stokes equations for alpha < alpha(L)(n). The energy is critical under scale transformations only for alpha = alpha(L)(n).
Title: Home range evolution and its implication in population outbreaks
Author(s): Araujo, SBL (Araujo, S. B. L.); Viswanathan, GM (Viswanathan, G. M.); de Aguiar, MAM (de Aguiar, M. A. M.)
Source: PHILOSOPHICAL TRANSACTIONS OF THE ROYAL SOCIETY A-MATHEMATICAL PHYSICAL AND ENGINEERING SCIENCES Volume: 368 Issue: 1933 Pages: 5661-5677 DOI: 10.1098/rsta.2010.0270 Published: DEC 28 2010
Abstract: We investigated the phenomenon of population outbreaks in a spatial predator-prey model, and we found that pattern formation and outbreaks occur if the predators have a limited neighbourhood of interaction with the preys. The outbreaks can display a scale-invariant power-law tail, indicating self-organized criticality. We have also studied the system from an evolutionary point of view, where the predator home range is a hereditary trait subjected to mutations. We found that mutation drives the predator home range area to an optimal value where pattern formation and outbreaks are still present, but the latter are much less frequent. We developed analytical approximations using mean field and pair correlation techniques that indicate that the predation strategy is crucial for existence of this optimal home range area.
Title: ECOLOGY Fish in Levy-flight foraging
Author(s): Viswanathan, GM (Viswanathan, Gandhimohan M.)
Source: NATURE Volume: 465 Issue: 7301 Pages: 1018-1019 DOI: 10.1038/4651018a Published: JUN 24 2010
Title: Anomalous diffusion in non-Markovian walks having amnestically induced persistence
Author(s): Ferreira, AS (Ferreira, A. S.); Cressoni, JC (Cressoni, J. C.); Viswanathan, GM (Viswanathan, G. M.); da Silva, MAA (Alves da Silva, Marco Antonio)
Source: PHYSICAL REVIEW E Volume: 81 Issue: 1 Article Number: 011125 DOI: 10.1103/PhysRevE.81.011125 Part: Part 1 Published: JAN 2010
Abstract: We report numerically and analytically estimated values for the Hurst exponent for a recently proposed non-Markovian walk characterized by amnestically induced persistence. These results are consistent with earlier studies showing that log-periodic oscillations arise only for large memory losses of the recent past. We also report numerical estimates of the Hurst exponent for non-Markovian walks with diluted memory. Finally, we study walks with a fractal memory of the past for a Thue-Morse and Fibonacci memory patterns. These results are interpreted and discussed in the context of the necessary and sufficient conditions for the central limit theorem to hold.
Author(s): Felisberto, ML (Felisberto, M. L.); Passos, FS (Passos, F. S.); Ferreira, AS (Ferreira, A. S.); da Silva, MAA (da Silva, M. A. A.); Cressoni, JC (Cressoni, J. C.); Viswanathan, GM (Viswanathan, G. M.)
Source: EUROPEAN PHYSICAL JOURNAL B Volume: 72 Issue: 3 Pages: 427-433 DOI: 10.1140/epjb/e2009-00361-6 Published: DEC 2009
Abstract: Random walks can undergo transitions from normal diffusion to anomalous diffusion as some relevant parameter varies, for instance the L,vy index in L,vy flights. Here we derive the Fokker-Planck equation for a two-parameter family of non-Markovian random walks with amnestically induced persistence. We investigate two distinct transitions: one order parameter quantifies log-periodicity and discrete scale invariance in the first moment of the propagator, whereas the second order parameter, known as the Hurst exponent, describes the growth of the second moment. We report numerical and analytical results for six critical exponents, which together completely characterize the properties of the transitions. We find that the critical exponents related to the diffusion-superdiffusion transition are identical in the positive feedback and negative feedback branches of the critical line, even though the former leads to classical superdiffusion whereas the latter gives rise to log-periodic superdiffusion.
Title: The random search problem: trends and perspectives PREFACE
Author(s): da Luz, MGE (da Luz, Marcos G. E.); Grosberg, A (Grosberg, Alexander); Raposo, EP (Raposo, Ernesto P.); Viswanathan, GM (Viswanathan, Gandhi M.)
Source: JOURNAL OF PHYSICS A-MATHEMATICAL AND THEORETICAL Volume: 42 Issue: 43 Article Number: 200301 DOI: 10.1088/0264-9381/26/20/200301 Published: OCT 30 2009
Title: Levy flights and random searches
Author(s): Raposo, EP (Raposo, E. P.); Buldyrev, SV (Buldyrev, S. V.); da Luz, MGE (da Luz, M. G. E.); Viswanathan, GM (Viswanathan, G. M.); Stanley, HE (Stanley, H. E.)
Source: JOURNAL OF PHYSICS A-MATHEMATICAL AND THEORETICAL Volume: 42 Issue: 43 Article Number: 434003 DOI: 10.1088/1751-8113/42/43/434003 Published: OCT 30 2009
Abstract: In this work we discuss some recent contributions to the random search problem. Our analysis includes superdiffusive Levy processes and correlated random walks in several regimes of target site density, mobility and revisitability. We present results in the context of mean-field-like and closed-form average calculations, as well as numerical simulations. We then consider random searches performed in regular lattices and lattices with defects, and we discuss a necessary criterion for distinguishing true superdiffusion from correlated random walk processes. We invoke energy considerations in relation to critical survival states on the edge of extinction, and we analyze the emergence of Levy behavior in deterministic search walks. Finally, we comment on the random search problem in the context of biological foraging.
Title: Can collective searches profit from Levy walk strategies?
Author(s): Santos, MC (Santos, M. C.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.); da Luz, MGE (da Luz, M. G. E.)
Source: JOURNAL OF PHYSICS A-MATHEMATICAL AND THEORETICAL Volume: 42 Issue: 43 Article Number: 434017 DOI: 10.1088/1751-8113/42/43/434017 Published: OCT 30 2009
Abstract: We address the problem of collective searching in which a group of walkers, guided by a leader, looks for randomly located target sites. In such a process, the necessity to maintain the group aggregated imposes a constraint in the foraging dynamics. We discuss four different models for the system collective behavior, with the leader and followers performing Gaussian as well as truncated Levy walks. In environments with low density of targets we show that Levy foraging is advantageous for the whole group, when compared with Gaussian strategy. Furthermore, certain extra rules must be incorporated in the individuals’ dynamics, so that a compromise between the trend to keep the group together and the global efficiency of search is met. The exact character of these rules depends on specific details of the foraging process, such as regeneration of target sites and energy costs.
Title: Multifractal detrended fluctuation analysis of analog random multiplicative processes
Author(s): Silva, LBM (Silva, L. B. M.); Vermelho, MVD (Vermelho, M. V. D.); Lyra, ML (Lyra, M. L.); Viswanathan, GM (Viswanathan, G. M.)
Source: CHAOS SOLITONS & FRACTALS Volume: 41 Issue: 5 Pages: 2806-2811 DOI: 10.1016/j.chaos.2008.10.027 Published: SEP 15 2009
Abstract: We investigate non-Gaussian statistical properties of stationary stochastic signals generated by an analog circuit that simulates a random multiplicative process with weak additive noise. The random noises are originated by thermal shot noise and avalanche processes, while the multiplicative process is generated by a fully analog circuit. The resulting signal describes stochastic time series of current interest in several areas such as turbulence, finance, biology and environment, which exhibit power-law distributions. Specifically, we study the correlation properties of the signal by employing a detrended fluctuation analysis and explore its multifractal nature. The singularity spectrum is obtained and analyzed as a function of the control circuit parameter that tunes the asymptotic power-law form of the probability distribution function. (C) 2008 Elsevier Ltd. All rights reserved.
Title: Hurst exponents for interacting random walkers obeying nonlinear Fokker-Planck equations
Author(s): Kumar, N (Kumar, Niraj); Viswanathan, GM (Viswanathan, G. M.); Kenkre, VM (Kenkre, V. M.)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 388 Issue: 18 Pages: 3687-3694 DOI: 10.1016/j.physa.2009.05.015 Published: SEP 15 2009
Abstract: Anomalous diffusion of random walks has been extensively studied for the case of non-interacting particles. Here we Study the evolution of nonlinear partial differential equations by interpreting them as Fokker-Planck equations arising from interactions among random walkers. We extend the formalism of generalized Hurst exponents to the Study of nonlinear evolution equations and apply it to several illustrative examples. They include an analytically solvable case of a nonlinear diffusion constant and three nonlinear equations which are not analytically solvable: the usual Fisher equation which contains a quadratic nonlinearity, a generalization of the Fisher equation with density-dependent diffusion constant, and the Nagumo equation which incorporates a cubic rather than a quadratic nonlinearity. We estimate the generalized Hurst exponents. (C) 2009 Elsevier B.V. All rights reserved.
Author(s): Agnaldo, JS (Agnaldo, J. S.); Cressoni, JC (Cressoni, J. C.); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICAL REVIEW B Volume: 79 Issue: 3 Article Number: 035308 DOI: 10.1103/PhysRevB.79.035308 Published: JAN 2009
Abstract: We propose a linearizable model for the nonlinear photocurrent-voltage characteristics of dye-sensitized nanocrystalline TiO2 photoelectrochemical solar cells. We solve the model and report theoretically predicted values for fill factors. A single free parameter of the model controls the fill factor. Upon renormalization, diverse experimental current-voltage data collapse onto a single universal function. The theoretical underpinning provides insight into physical mechanisms responsible for the large fill factors as well as their known dependence on the open circuit voltage. These advances allow the estimation of the complete current-voltage curve and fill factor from any three experimental data points, e.g., the open circuit voltage, the short circuit current, and one other intermediate measurement.
Author(s): Viswanathan, GM (Viswanathan, G. M.); Viswanathan, TM (Viswanathan, T. M.)
Source: EPL Volume: 84 Issue: 5 Article Number: 50006 DOI: 10.1209/0295-5075/84/50006 Published: DEC 2008
Abstract: We investigate the formation of singularities in incompressible. flows governed by Navier-Stokes equations in d >= 2 dimensions with a fractional Laplacian vertical bar del vertical bar(alpha). We derive analytically a sufficient but not necessary condition for the solutions to remain always smooth and show that. finite-time singularities cannot form for alpha >= alpha(c) = 1 + d/2. Moreover, initial singularities become unstable for alpha > alpha(c). The scale invariance symmetry intrinsic to the Navier-Stokes system becomes spontaneously broken, except at the critical point alpha = alpha(c). Copyright (C) EPLA, 2008
Title: Multifractality of random walks in the theory of vehicular traffic
Author(s): Buendia, GM (Buendia, G. M.); Viswanathan, GM (Viswanathan, G. M.); Kenkre, VM (Kenkre, V. M.)
Source: PHYSICAL REVIEW E Volume: 78 Issue: 5 Article Number: 056110 DOI: 10.1103/PhysRevE.78.056110 Part: Part 2 Published: NOV 2008
Abstract: We investigate the origin of the experimentally observed multifractal scaling of vehicular traffic flows by studying a hydrodynamic model of traffic. We first extend and apply the formalism of generalized Hurst exponents H(q) to the case of random walkers that not only diffuse but rather also undergo nonlinear convection due to interactions with other walkers. We recover analytically, as expected, that H(q) equals 1/2 for a single random walker starting at the origin whose probability density function satisfies Burger’s equation. Despite this result for a single walker, we find that for a collection of nonlinearly convecting diffusive particles, transient effects can give rise to multiscaling at given time scales for many initial conditions. In the Lighthill-Whitham-Richards hydrodynamic model of traffic, this multiscaling effect becomes more prominent for smaller diffusion constants and larger speed limits. We discuss the relevance of these findings for the realistic scenario of traffic that flows from small roads to large highways and vice versa, where transient effects can be expected to play a significant role.
Title: Levy flights and superdiffusion in the context of biological encounters and random searches
Author(s): Viswanathan, GM (Viswanathan, G. M.); Raposo, EP (Raposo, E. P.); da Luz, MGE (da Luz, M. G. E.)
Source: PHYSICS OF LIFE REVIEWS Volume: 5 Issue: 3 Pages: 133-150 DOI: 10.1016/j.plrev.2008.03.002 Published: SEP 2008
Abstract: We review the general problem of random searches in the context of biological encounters. We analyze deterministic and stochastic aspects of searching in general and address the destructive and nondestructive cases specifically. We discuss the concepts of Levy walks as adaptive strategies and explore possible examples. We also review Levy searches in other media and spaces, including lattices and networks as opposed to continuous environments. We analyze empirical evidence supporting the Levy night foraging hypothesis, as well as the more general idea of superdiffusive foraging. We compare these hypothesis with alternative theories of random searches. Finally, we comment on several issues relevant to the practical application of models of Levy and superdiffusive strategies to the general question of biological foraging. (C) 2008 Elsevier B.V. All rights reserved.
Title: The influence of turning angles on the success of non-oriented animal searches
Author(s): Bartumeus, F (Bartumeus, F.); Catalan, J (Catalan, J.); Viswanathan, GM (Viswanathan, G. M.); Raposo, EP (Raposo, E. P.); da Luz, MGE (da Luz, M. G. E.)
Source: JOURNAL OF THEORETICAL BIOLOGY Volume: 252 Issue: 1 Pages: 43-55 DOI: 10.1016/j.jtbi.2008.01.009 Published: MAY 7 2008
Abstract: Animal searches cover a full range of possibilities from highly deterministic to apparently completely random behaviors. However, even those stochastic components of animal movement can be adaptive, since not all random distributions lead to similar success in finding targets. Here we address the general problem of optimizing encounter rates in non-deterministic, non-oriented searches, both in homogeneous and patchy target landscapes. Specifically, we investigate how two different features related to turning angle distributions influence encounter success: (i) the shape (relative kurtosis) of the angular distribution and (ii) the correlations between successive relative orientations (directional memory). Such influence is analyzed in correlated random walk models using a proper choice of representative turning angle distributions of the recently proposed Jones and Pewsey class. We consider the cases of distributions with nearly the same shape but considerably distinct correlation lengths, and distributions with same correlation but with contrasting relative kurtosis. In homogeneous landscapes, we find that the correlation length has a large influence in the search efficiency. Moreover, similar search efficiencies can be reached by means of distinctly shaped turning angle distributions, provided that the resulting correlation length is the same. In contrast, in patchy landscapes the particular shape of the distribution also becomes relevant for the search efficiency, specially at high target densities. Excessively sharp distributions generate very inefficient searches in landscapes where local target density fluctuations are large. These results are of evolutionary interest. On the one hand, it is shown that equally successful directional memory can arise from contrasting turning behaviors, therefore increasing the likelihood of robust adaptive stochastic behavior. On the other hand, when target landscape is patchy, adequate tumbling may help to explore better local scale heterogeneities, being some details of the shape of the distribution also potentially adaptive. (c) 2008 Elsevier Ltd. All rights reserved.
Title: Spontaneous symmetry breaking in amnestically induced persistence
Author(s): da Silva, MAA (Alves da Silva, Marco Antonio); Viswanathan, GM (Viswanathan, G. M.); Ferreira, AS (Ferreira, A. S.); Cressoni, JC (Cressoni, J. C.)
Source: PHYSICAL REVIEW E Volume: 77 Issue: 4 Article Number: 040101 DOI: 10.1103/PhysRevE.77.040101 Part: Part 1 Published: APR 2008
Abstract: We investigate a recently proposed non-Markovian random walk model characterized by loss of memories of the recent past and amnestically induced persistence. We report numerical and analytical results showing the complete phase diagram, consisting of four phases, for this system: (i) classical nonpersistence, (ii) classical persistence, (iii) log-periodic nonpersistence, and (iv) log-periodic persistence driven by negative feedback. The first two phases possess continuous scale invariance symmetry, however, log-periodicity breaks this symmetry. Instead, log-periodic motion satisfies discrete scale invariance symmetry, with complex rather than real fractal dimensions. We find for log-periodic persistence evidence not only of statistical but also of geometric self-similarity.
Title: Optimization of random searches on defective lattice networks
Author(s): Santos, MC (Santos, M. C.); Viswanathan, GM (Viswanathan, G. M.); Raposo, EP (Raposo, E. P.); da Luz, MGE (da Luz, M. G. E.)
Source: PHYSICAL REVIEW E Volume: 77 Issue: 4 Article Number: 041101 DOI: 10.1103/PhysRevE.77.041101 Part: Part 1 Published: APR 2008
Abstract: We study the general problem of how to search efficiently for targets randomly located on defective lattice networks-i.e., regular lattices which have some fraction of its nodes randomly removed. We consider large but finite triangular lattices and assume for the search dynamics that the walker chooses steps lengths l(j) from the power-law distribution P(l(j))similar to l(j)(-mu), with the exponent mu regulating the strategy of the search process. At each step l(j), the searcher moves in straight lines and constantly looks within a detection radius of vision r(v) for the targets along the way. If there is contact with a defect, the movement stops and a new step length is chosen. Hence, the presence of defects decreases the efficiency of the overall process. We study numerically how three different aspects of the lattice influence the optimization of the search efficiency: (i) the type of boundary conditions, (ii) the concentration of targets and defects, and (iii) the category or class of search-destructive, nondestructive, or regenerative. Motivated by the results, we develop a type of mean-field model for the problem and obtain an analytical approximation for the search efficiency function. Finally we discuss, in the context of searches, how defective lattices compare with perfect lattices and with continuous environments.
Title: Log-periodic precursors to catastrophic events: the 1999 crash as a case study
Author(s): Juliao, CJS (Juliao, C. J. S.); Gleria, I (Gleria, Iram); Cavalcanti, S (Cavalcanti, Solange); Viswanathan, GM (Viswanathan, G. M.)
Source: REVISTA BRASILEIRA DE ENSINO DE FISICA Volume: 30 Issue: 2 Article Number: 2303 Published: APR-JUN 2008
Abstract: Large earthquakes, rupture in complex materials, stock market crashes: all can be viewed as catastrophes – the sudden transition from a quit state to crisis. Would it be possible to forecast the events? A unified framework for the modeling and forecasting of catastrophes was proposed by D. Sornette, based on the concept of log-periodicity. In this article we discus the potential for predictability of this theory and we illustrate it in problems related to stock market crashes. We study this method of forecasting applied to the stock market index of the BOVESPA Sao Paulo Stock Exchange. IBOVESPA. We seek evidence of log-periodic behavior, comparing a period without crashes to the period before the crash of 14 January 1999. The efficiency and the relative simplicity of the method serve as incentive to undergraduate students eager to see the theory being put to practice.
Title: Multifractality and heteroscedastic dynamics: An application to time series analysis
Author(s): Nascimento, CM (Nascimento, C. M.); Junior, HBN (Junior, H. B. N.); Jennings, HD (Jennings, H. D.); Serva, M (Serva, M.); Gleria, I (Gleria, Iram); Viswanathan, GM (Viswanathan, G. M.)
Source: EPL Volume: 81 Issue: 1 Article Number: 18002 DOI: 10.1209/0295-5075/81/18002 Published: 2008
Abstract: An increasingly important problem in physics concerns scale invariance symmetry in diverse complex systems, often characterized by heteroscedastic dynamics. We investigate the nature of the relationship between the heteroscedastic and fractal aspects of the dynamics of complex systems, by analyzing the sensitivity to heteroscedasticity of the scaling properties of weakly nonstationary time series. By using multifractal detrended fluctuation analysis, we study the singularity spectra of currency exchange rate fluctuations, after partially or completely eliminating n-point correlations via data shuffling techniques. We conclude that heteroscedasticity can significantly increase multifractality and interpret these findings in the context of self-organizing and adaptive complex systems. Copyright (C) EPLA, 2008.
Title: The Levy sections theorem: An application to econophysics
Author(s): Figueiredo, A (Figueiredo, A.); Matsushita, R (Matsushita, R.); daSilva, S (daSilva, S.); Serva, M (Serva, M.); Viswanathan, GM (Viswanathan, G. M.); Nascimento, C (Nascimento, C.); Gleria, I (Gleria, Iram)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 386 Issue: 2 Pages: 756-759 DOI: 10.1016/j.physa.2007.08.042 Published: DEC 15 2007
Abstract: We employ the Levy sections theorem in the analysis of selected dollar exchange rate time series. The theorem is an extension of the classical central limit theorem and offers an alternative to the most usual analysis of the sum variable. We find that the presence of fat tails can be related to the local volatility pattern of the series. (c) 2007 Elsevier B.V. All rights reserved.
Title: Revisiting Levy flight search patterns of wandering albatrosses, bumblebees and deer
Author(s): Edwards, AM (Edwards, Andrew M.); Phillips, RA (Phillips, Richard A.); Watkins, NW (Watkins, Nicholas W.); Freeman, MP (Freeman, Mervyn P.); Murphy, EJ (Murphy, Eugene J.); Afanasyev, V (Afanasyev, Vsevolod); Buldyrev, SV (Buldyrev, Sergey V.); da Luz, MGE (da Luz, M. G. E.); Raposo, EP (Raposo, E. P.); Stanley, HE (Stanley, H. Eugene); Viswanathan, GM (Viswanathan, Gandhimohan M.)
Source: NATURE Volume: 449 Issue: 7165 Pages: 1044-U5 DOI: 10.1038/nature06199 Published: OCT 25 2007
Abstract: The study of animal foraging behaviour is of practical ecological importance(1), and exemplifies the wider scientific problem of optimizing search strategies(2). Levy flights are random walks, the step lengths of which come from probability distributions with heavy power-law tails(3,4), such that clusters of short steps are connected by rare long steps. Levy flights display fractal properties, have no typical scale, and occur in physical(3-5) and chemical(6) systems. An attempt to demonstrate their existence in a natural biological system presented evidence that wandering albatrosses perform Levy flights when searching for prey on the ocean surface(7). This well known finding(2,4,8,9) was followed by similar inferences about the search strategies of deer(10) and bumblebees(10). These pioneering studies have triggered much theoretical work in physics (for example, refs 11, 12), as well as empirical ecological analyses regarding reindeer(13), microzooplankton(14), grey seals(15), spider monkeys(16) and fishing boats(17). Here we analyse a new, high-resolution data set of wandering albatross flights, and find no evidence for Levy flight behaviour. Instead we find that flight times are gamma distributed, with an exponential decay for the longest flights. We re-analyse the original albatross data(7) using additional information, and conclude that the extremely long flights, essential for demonstrating Levy flight behaviour, were spurious. Furthermore, we propose a widely applicable method to test for power-law distributions using likelihood(18) and Akaike weights(19,20). We apply this to the four original deer and bumblebee data sets(10), finding that none exhibits evidence of Levy flights, and that the original graphical approach(10) is insufficient. Such a graphical approach has been adopted to conclude Levy flight movement for other organisms(13-17), and to propose Levy flight analysis as a potential real-time ecosystem monitoring tool(17). Our results question the strength of the empirical evidence for biological Levy flights.
Title: Why stock markets crash: the origin of fat tailed distributions of returns
Author(s): do Nascimento, HB (do Nascimento, H. B.); Fulco, UL (Fulco, U. L.); Lyra, ML (Lyra, M. L.); Serva, M (Serva, M.); Viswanathan, GM (Viswanathan, G. M.)
Source: REVISTA BRASILEIRA DE ENSINO DE FISICA Volume: 29 Issue: 3 Pages: 341-346 Published: JUL-OCT 2007
Abstract: An important problem in physics concerns the origin of very large events in the dynamics of complex systems, such as large earthquakes, pandemics, mass extinctions and financial crashes. Here we review recent advances that suggest that the largest events in the dynamics of stock markets are due to long-range memory effects. We have studied the distributions of stock returns measured over different time lags tau and compared the results with those obtained after shuffling the data to reduce the memory. Specifically, destroying all correlations by shuffling the order of the returns, but without changing the tau = 1 d distribution, significantly reduces the probability of very large events. The distribution of returns for tau > 1 d loses the fat tails and acquires a more Gaussian shape. However, shuffling only the signs-but not the modulus-of the returns allows the fat tails and large events to persist for tau > 1 d. From these results, one can conclude that the very large events are caused by known multifractal long-range correlations in the modulus of the financial time series.
Title: Origin of power-law distributions in deterministic walks: The influence of landscape geometry
Author(s): Santos, MC (Santos, M. C.); Boyer, D (Boyer, D.); Miramontes, O (Miramontes, O.); Viswanathan, GM (Viswanathan, G. M.); Raposo, EP (Raposo, E. P.); Mateos, JL (Mateos, J. L.); da Luz, MGE (da Luz, M. G. E.)
Source: PHYSICAL REVIEW E Volume: 75 Issue: 6 Article Number: 061114 DOI: 10.1103/PhysRevE.75.061114 Part: Part 1 Published: JUN 2007
Abstract: We investigate the properties of a deterministic walk, whose locomotion rule is always to travel to the nearest site. Initially the sites are randomly distributed in a closed rectangular (A/LxL) landscape and, once reached, they become unavailable for future visits. As expected, the walker step lengths present characteristic scales in one (L -> 0) and two (A/L similar to L) dimensions. However, we find scale invariance for an intermediate geometry, when the landscape is a thin striplike region. This result is induced geometrically by a dynamical trapping mechanism, leading to a power-law distribution for the step lengths. The relevance of our findings in broader contexts-of both deterministic and random walks-is also briefly discussed.
Title: Amnestically induced persistence in random walks
Author(s): Cressoni, JC (Cressoni, J. C.); da Silva, MAA (Alves da Silva, Marco Antonio); Viswanathan, GM (Viswanathan, G. M.)
Source: PHYSICAL REVIEW LETTERS Volume: 98 Issue: 7 Article Number: 070603 DOI: 10.1103/PhysRevLett.98.070603 Published: FEB 16 2007
Abstract: We study how the Hurst exponent alpha depends on the fraction f of the total time t remembered by non-Markovian random walkers that recall only the distant past. We find that otherwise nonpersistent random walkers switch to persistent behavior when inflicted with significant memory loss. Such memory losses induce the probability density function of the walker’s position to undergo a transition from Gaussian to non-Gaussian. We interpret these findings of persistence in terms of a breakdown of self-regulation mechanisms and discuss their possible relevance to some of the burdensome behavioral and psychological symptoms of Alzheimer’s disease and other dementias.
Title: Search dynamics at the edge of extinction: Anomalous diffusion as a critical survival state
Author(s): Faustino, CL (Faustino, C. L.); da Silva, LR (da Silva, L. R.); da Luz, MGE (da Luz, M. G. E.); Raposo, EP (Raposo, E. P.); Viswanathan, GM (Viswanathan, G. M.)
Source: EPL Volume: 77 Issue: 3 Article Number: 30002 DOI: 10.1209/0295-5075/77/30002 Published: 2007
Abstract: We investigate the general problem of autonomous random walkers whose sole source of energy are search targets that are themselves diffusing random walkers. We study how the energy accumulated by the searcher varies with the target density via numerical simulations and compare the results with an analytical model for fixed targets. We report that superdiffusion of either searcher or target confers substantial energetic advantages to the former. While superdiffusion may not play a crucial role for high target densities, in contrast it confers a vital advantage in the limit of low densities at the edge of extinction: diffusive searchers rapidly die but superdiffusive searchers can survive for long periods without entering into the extinction state. The validity and relevance of our findings in broader contexts are also discussed.
Author(s): Giuggioli, L (Giuggioli, L.); Viswanathan, GM (Viswanathan, G. M.); Kenkre, VM (Kenkre, V. M.); Parmenter, RR (Parmenter, R. R.); Yates, TL (Yates, T. L.)
Source: EPL Volume: 77 Issue: 4 Article Number: 40004 DOI: 10.1209/0295-5075/77/40004 Published: 2007
Abstract: We investigate the general problem of how the finiteness of a probing window for measurements of the movements of a random walker can lead to spurious detection of multifractality as well as to incorrect values of Hurst exponents, and propose a method for correcting for these effects. We also study the case in which the roaming region of the walker is itself of limited extent, when a nonlinear interplay occurs between the roaming area and the window size. In the context of animal movements, we describe briefly an application of these ideas to mark-recapture observations in a mouse population, of interest to the important topic of the spread of the Hantavirus epidemic. Copyright (C) EPLA, 2007.
Title: Discrete-time non-Markovian random walks: The effect of memory limitations on scaling
Author(s): da Silva, MAA (da Silva, MAA); Cressoni, JC (Cressoni, JC); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 364 Pages: 70-78 DOI: 10.1016/j.physa.2005.08.066 Published: MAY 15 2006
Abstract: An important class of random walks includes those in which the random increment at time step t depends on the complete history of the process. We consider a recently proposed discrete-time non-Markovian random walk process characterized by a memory parameter p. We numerically calculate the first and second moments of the position distribution and relate our results to known analytic results for special cases. We obtain data collapse for the position distribution. We study the effect of reducing the memory by considering a modified model in which only a fraction f of the previous steps are remembered. Surprisingly, the behavior becomes Markovian for small f, even though the correlation time diverges for f > 0. We also study the transient effects near the memory edge by considering a Markovian limit of the original model. We observe a crossover to Markovian behavior for times much larger than the range of the memory. (c) 2005 Elsevier B.V. All rights reserved.
Title: TiO2 dye sensitized solar cells
Author(s): JS Agnaldo, JBV Bastos, JC Cressoni, GM Viswanathan
Source: Revista Brasileira de Ensino de Física Volume 28, Pages 77-84 DOI: 10.1590/S1806-11172006000100010 Published
Abstract: Grätzel solar cells consist of nanocrystalline dye sensitized TiO2 photovoltaic cells. Such cells contain a nanoporous surface of TiO2, which is a wide bandgap semiconductor. The light excites electrons from the dye which are then injected into the conduction band of the TiO2. This electrochemical process is regenerative, with part of the converted energy being lost due to charge recombination. Understanding this recombination process is an important step for the development of more efficient cells. We make a suggestion for an experiment for undergraduate physics laboratory classes using such solar cells and we show that the efficiency increases along with the growth of the value of the internal resistance of recombination.
Title: A Markov model of financial returns
Author(s): Serva, M (Serva, M); Fujco, UL (Fujco, UL); Gleria, IM (Gleria, IM); Lyra, ML (Lyra, ML); Petroni, F (Petroni, F); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 363 Issue: 2 Pages: 393-403 DOI: 10.1016/j.physa.2005.08.070 Published: MAY 1 2006
Abstract: We address the general problem of how to quantify the kinematics of time series with stationary first moments but having non stationary multifractal long-range correlated second moments. We show that a Markov process is sufficient to model important aspects of the multifractality observed in financial time series and propose a kinematic model of price fluctuations. We test the proposed model by analyzing index closing prices of the New York Stock Exchange and the DEM/USD tick-by-tick exchange rates obtained from Reuters EFX. We show that the model captures the characteristic features observed in actual financial time series, including volatility clustering, time scaling and fat tails in the probability density functions, power-law behavior of volatility correlations and, most importantly, the observed nonuniversal multifractal singularity spectrum. Motivated by our finding of strong agreement between the model and the data, we argue that at least two independent stochastic Gaussian variables are required to adequately model price fluctuations. (c) 2005 Elsevier B.V. All rights reserved.
Title: Animal search strategies: A quantitative. random-walk analysis
Author(s): Bartumeus, F (Bartumeus, F); Da Luz, MGE (Da Luz, MGE); Viswanathan, GM (Viswanathan, GM); Catalan, J (Catalan, J)
Source: ECOLOGY Volume: 86 Issue: 11 Pages: 3078-3087 DOI: 10.1890/04-1806 Published: NOV 2005
Abstract: Recent advances in spatial ecology have improved our understanding of the role of large-scale animal movements. However, an unsolved problem concerns the inherent stochasticity involved in many animal search displacements and its possible adaptive value. When animals have no information about where targets (i.e., resource patches, mates, etc.) are located, different random search strategies may provide different chances to find them. Assuming random-walk models as a necessary tool to understand how animals face such environmental uncertainty, we analyze the statistical differences between two random-walk models commonly used to fit animal movement data, the Levy walks and the correlated random walks, and we quantify their efficiencies (i.e., the number of targets found in relation to total displacement) within a random search context. Correlated random-walk properties (i.e., scale-finite correlations) may be interpreted as the by-product of locally scanning mechanisms. Levy walks, instead, have fundamental properties (i.e., super-diffusivity and scale invariance) that allow a higher efficiency in random search scenarios. Specific biological mechanisms related to how animals punctuate their movement with sudden reorientations in a random search would be sufficient to, sustain Levy walk properties. Furthermore, we investigate a new model (the Levy-modulated correlated random walk) that combines the properties of correlated and Levy walks. This model shows that Levy walk properties are robust to any behavioral mechanism providing short-range correlations in the walk. We propose that some animals may have evolved the. ability of performing Levy walks as adaptive strategies in order to face search uncertainties.
Title: Optimization of random searches on regular lattices
Author(s): Santos, MC (Santos, MC); Viswanathan, GM (Viswanathan, GM); Raposo, EP (Raposo, EP); da Luz, MGE (da Luz, MGE)
Source: PHYSICAL REVIEW E Volume: 72 Issue: 4 Article Number: 046143 DOI: 10.1103/PhysRevE.72.046143 Part: Part 2 Published: OCT 2005
Abstract: We investigate random searches on isotropic and topologically regular square and triangular lattices with periodic boundary conditions and study the efficiency of search strategies based on a power-law distribution P(l)similar to l(-mu) of step lengths l. We consider both destructive searches, in which a target can be visited only once, and nondestructive searches, when a target site is always available for future visits. We discuss (i) the dependence of the search efficiency on the choice of the lattice topology, (ii) the relevance of the periodic boundary conditions, (iii) the behavior of the optimal power-law exponent mu(opt) as a function of target site density, (iv) the differences between destructive and nondestructive environments, and finally (v) how the results for the discrete searches differ from the continuous cases previously studied.
Title: Necessary criterion for distinguishing true superdiffusion from correlated random walk processes
Author(s): Viswanathan, GM (Viswanathan, GM); Raposo, EP (Raposo, EP); Bartumeus, F (Bartumeus, F); Catalan, J (Catalan, J); da Luz, MGE (da Luz, MGE)
Source: PHYSICAL REVIEW E Volume: 72 Issue: 1 Article Number: 011111 DOI: 10.1103/PhysRevE.72.011111 Part: Part 1 Published: JUL 2005
Abstract: A difficulty in interpreting phenomena related to anomalous diffusion concerns how to identify scale invariant superdiffusive from Markovian correlated random walk processes. Here we propose a criterion that can distinguish between these two kinds of random walks and describe its usefulness in interpreting real data. To do so, we estimate the correlation time tau of the orientation persistence of a general correlated random walk. If the experimentally observed random walk appears diffusive on scales larger than tau, then the data cannot support the possibility of superdiffusion. We argue that the criterion is a necessary but not sufficient condition for establishing true superdiffusive behavior.
Title: Critical behavior of an epidemic model of drug resistant diseases
Author(s): Da Silva, CR (Da Silva, CR); Fulco, UL (Fulco, UL); Lyra, ML (Lyra, ML); Viswanathan, GM (Viswanathan, GM)
Source: INTERNATIONAL JOURNAL OF MODERN PHYSICS C Volume: 15 Issue: 9 Pages: 1279-1290 DOI: 10.1142/S0129183104006704 Published: NOV 2004
Abstract: In this work, we study the critical behavior of an epidemic propagation model that considers individuals that can develop drug resistance. In our lattice model, each site can be found in one of the four states: empty, healthy, normally infected (not drug resistant) and strain infected (drug resistant) states. The most relevant parameters in our model are related to the mortality, cure and mutation rates. This model presents two distinct stationary active phases: a phase with co-existing normal and drug resistant infected individuals, and an intermediate active phase with only drug resistant individuals. We employed a finite-size scaling analysis to compute the critical points and the critical exponents, beta/nu and 1/nu, governing the phase transitions between these active states and the absorbing inactive state. Our results are consistent with the hypothesis that these transitions belong to the directed percolation universality class.
Author(s): Santos, MC (Santos, MC); Raposo, EP (Raposo, EP); Viswanathan, GM (Viswanathan, GM); da Luz, MGE (da Luz, MGE)
Source: EUROPHYSICS LETTERS Volume: 67 Issue: 5 Pages: 734-740 DOI: 10.1209/epl/i2004-10114-9 Published: SEP 2004
Abstract: One of the most important aspects in the general search problem of finding randomly located target sites concerns how to characterize the role played by the non-revisit ability delay time T during which a previously found target becomes unavailable to the searcher. By using an appropriate parameterization of the number of random walk steps undertaken between successive targets, we show that for the case of sparse randomly distributed sites the optimal search strategy shifts from a superdiffusive to a ballistic strategy consisting of essentially rectilinear motion between the targets, as T increases from tau –> 0 to tau –> infinity, respectively. The crossover between these limiting regimes occurs as a function of tau. These conclusions are shown to hold even if dissipative phenomena are considered in the searching dynamics. We discuss the results in the context of their application to animal foraging.
Title: Variance fluctuations in nonstationary time series: a comparative study of music genres
Author(s): Jennings, HD (Jennings, HD); Ivanov, PC (Ivanov, PC); Martins, AD (Martins, AD); da Silva, PC (da Silva, PC); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 336 Issue: 3-4 Pages: 585-594 DOI: 10.1016/j.physa.2003.12.049 Published: MAY 15 2004
Abstract: An important problem in physics concerns the analysis of audio time series generated by transduced acoustic phenomena. Here,. we develop a new method to quantify the scaling properties of the local variance of nonstationary time series. We apply this technique to analyze audio signals obtained from selected genres of music. We find quantitative differences in the correlation properties of high art music, popular music, and dance music. We discuss the relevance of these objective findings in relation to the subjective experience of music. (C) 2003 Elsevier B.V. All rights reserved.
Title: A stochastic model for multifractal behavior of stock prices
Author(s): Fulco, UL (Fulco, UL); Lyra, ML (Lyra, ML); Petroni, F (Petroni, F); Serva, M (Serva, M); Viswanathan, GM (Viswanathan, GM)
Source: INTERNATIONAL JOURNAL OF MODERN PHYSICS B Volume: 18 Issue: 4-5 Pages: 681-689 DOI: 10.1142/S0217979204024306 Published: FEB 20 2004
Abstract: We investigate the general problem of how to model the kinematics of stock prices without considering the dynamical causes of motion. We propose a Markovian stochastic process which is able to reproduce the experimentally observed volatility clustering and fat tails in the probability density functions (PDF) of financial time series. More importantly, the process also reproduces the PDF time scaling, the power law memory of volatility and the apparent multifractality of the time series up to the time scale which is experimentally observable.
Title: Dynamical robustness of Levy search strategies
Author(s): Raposo, EP (Raposo, EP); Buldyrev, SV (Buldyrev, SV); da Luz, MGE (da Luz, MGE); Santos, MC (Santos, MC); Stanley, HE (Stanley, HE); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICAL REVIEW LETTERS Volume: 91 Issue: 24 Article Number: 240601 DOI: 10.1103/PhysRevLett.91.240601 Published: DEC 12 2003
Abstract: We study the role of dynamical constraints in the general problem of finding the best statistical strategy for random searching when the targets can be detected only in the limited vicinity of the searcher. We find that the optimal search strategy depends strongly on the delay time tau during which a previously visited site becomes unavailable. We also find that the optimal search strategy is always described for large step lengths . by a power-law distribution P(.)similar to.(-mu), with 1<mu(tau)less than or equal to2. Our findings appear to remain valid even if arbitrary energy costs of locomotion are considered.
Title: The origin of fat-tailed distributions in financial time series
Author(s): Viswanathan, GM (Viswanathan, GM); Fulco, UL (Fulco, UL); Lyra, ML (Lyra, ML); Serva, M (Serva, M)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 329 Issue: 1-2 Pages: 273-280 DOI: 10.1016/S0378-4371(03)00608-3 Published: NOV 1 2003
Abstract: A classic problem in physics is the origin of fat-tailed distributions generated by complex systems. We study the distributions of stock returns measured over different time lags tau. We find that destroying all correlations without changing the tau = 1 d distribution, by shuffling the order of the daily returns, causes the fat tails to almost vanish for tau > 1 d. We argue that the fat tails are caused by the well-known long-range volatility correlations that have already been systematically studied previously. Indeed, destroying only sign correlations, by shuffling the order of only the signs (but not the absolute values) of the daily returns, allows the fat tails to persist for tau > 1 d. (C) 2003 Elsevier B.V. All rights reserved.
Title: Levy flight random searches in biological phenomena
Author(s): Viswanathan, GM (Viswanathan, GM); Bartumeus, F (Bartumeus, F); Buldyrev, SV (Buldyrev, SV); Catalan, J (Catalan, J); Fulco, UL (Fulco, UL); Havlin, S (Havlin, S); da Luz, MGE (da Luz, MGE); Lyra, ML (Lyra, ML); Raposo, EP (Raposo, EP); Stanley, HE (Stanley, HE)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 314 Issue: 1-4 Pages: 208-213 Article Number: DOI: 10.1016/S0378-4371(02)01157-3 Published: NOV 1 2002
Abstract: There has been growing interest in the study of Levy flights observed in the movements of biological organisms performing random walks while searching for other organisms. Here, we approach the problem of what is the best statistical strategy for optimizing the encounter rate between “searcher” and “target” organisms-either of the same or of different species-in terms of a limiting generalized searcher-target model (e.g., predator-prey, mating partner, pollinator-flower). In this context, we discuss known results showing that for fixed targets an inverse square density distribution of step lengths can optimize the encounter rate. For moving targets, we review how the encounter rate depends on whether organisms move in Levy or Brownian random walks. We discuss recent findings indicating that Levy walks confer a significant advantage for increasing encounter rates only when the searcher is larger or moves rapidly relative to the target, and when the target density is low. (C) 2002 Elsevier Science B.V. All rights reserved.
Title: Largest and second largest cluster statistics at the percolation threshold of hypercubic lattices
Author(s): da Silva, CR (da Silva, CR); Lyra, ML (Lyra, ML); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICAL REVIEW E Volume: 66 Issue: 5 Article Number: 056107 DOI: 10.1103/PhysRevE.66.056107 Published: NOV 2002
Abstract: We investigate the scale invariance of the average ratio between the masses of the largest and second largest clusters at percolation. We employ a finite size scaling method to estimate percolation thresholds based on the simulations of relatively small lattices, and report on estimates for p(c) in hypercubic lattices with d=2-7, in full agreement with the best literature estimates. Also, we find the critical mass ratio to be strongly dependent on the boundary conditions, decreasing with the lattice dimension. Further, we compute several relevant mass distribution functions associated with the two largest clusters, which approach to limiting distributions for d>6. Finally, we discuss the main relevant features of the mass distributions in light of the relative role played by the spanning and nonspanning clusters.
Author(s): Bartumeus, F (Bartumeus, F); Catalan, J (Catalan, J); Fulco, UL (Fulco, UL); Lyra, ML (Lyra, ML); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICAL REVIEW LETTERS Volume: 89 Issue: 10 Article Number: 109902 DOI: 10.1103/PhysRevLett.89.109902 Published: SEP 2 2002
Title: A semi-classical approach for hybrid ferromagnetic and antiferromagnetic superlattices
Author(s): Fulco, UL (Fulco, UL); Fulco, P (Fulco, P); Viswanathan, GM (Viswanathan, GM); Albuquerque, EL (Albuquerque, EL)
Source: PHYSICA STATUS SOLIDI B-BASIC RESEARCH Volume: 233 Issue: 2 Pages: 230-237 DOI: 10.1002/1521-3951(200209)233:2<230::AID-PSSB230>3.0.CO;2-9 Published: SEP 2002
Abstract: We present a semi-classical theory, based on the torque equation of motion for the magnetization, to investigate the spin wave spectra in magnetic superlattices, whose constituents are alternating ferromagnetic and antiferromagnetic layers. We consider the presence of an external magnetic field applied in the plane of the layers and parallel to the easy axis of the structure, supposed to be in the z-direction. By using a transfer-matrix approach, to simplify the algebra which is otherwise quite complex, we explicitly obtain the analytical expression for the spin wave’s dispersion relation. For numerical put-pose. we confine our discussion to uniaxial antiferromagnetic fluorides (e.g. MnF2), while the ferromagnetic material is considered to be EuS. We illustrate our theoretical results numerically. and compare them with previous works done by using a microscopic Heisenberg model.
Title: Optimizing the encounter rate in biological interactions: Levy versus Brownian strategies
Author(s): Bartumeus, F (Bartumeus, F); Catalan, J (Catalan, J); Fulco, UL (Fulco, UL); Lyra, ML (Lyra, ML); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICAL REVIEW LETTERS Volume: 88 Issue: 9 Article Number: 097901 DOI: 10.1103/PhysRevLett.88.097901 Published: MAR 4 2002
Abstract: An important application involving two-species reaction-diffusion systems relates to the problem of finding the best statistical strategy for optimizing the encounter rate between organisms. We investigate the general problem of how the encounter rate depends on whether organisms move in Levy or Brownian random walks. By simulating a limiting generalized searcher-target model (e.g., predator-prey, mating partner, pollinator-flower), we find that Levy walks confer a significant advantage for increasing encounter rates when the searcher is larger or moves rapidly relative to the target, and when the target density is low.
Title: Properties of Levy flights on an interval with absorbing boundaries
Author(s): Buldyrev, SV (Buldyrev, SV); Gitterman, M (Gitterman, M); Havlin, S (Havlin, S); Kazakov, AY (Kazakov, AY); da Luz, MGE (da Luz, MGE); Raposo, EP (Raposo, EP); Stanley, HE (Stanley, HE); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 302 Issue: 1-4 Pages: 148-161 DOI: 10.1016/S0378-4371(01)00461-7 Published: DEC 15 2001
Abstract: We consider a Levy flyer of order a that stalls from a point xo on an interval [0, L] with absorbing boundaries. We find a closed-form expression for an arbitrary average quantity, characterizing the trajectory of the flyer, such as mean first passage time, average total path length, probability to be absorbed by one of the boundaries. Using fractional differential equations with a Riesz kernel, we find exact analytical expressions for these quantities in the continuous limit. We find numerically the eigenfunctions and the eigenvalues of these equations. We study how the results of Monte-Carlo simulations of the Levy flights with different flight length distributions converge to the continuous approximations. We show that if x(0) is placed in the vicinity of absorbing boundaries, the average total path length has a minimum near alpha = 1, corresponding to the Cauchy distribution. We discuss the relevance of these results to the problem of biological foraging and transmission of light through cloudy atmosphere. (C) 2001 Elsevier Science B.V. All rights reserved.
Title: Average time spent by Levy flights and walks on an interval with absorbing boundaries
Author(s): Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); Kazakov, AY (Kazakov, AY); da Luz, MGE (da Luz, MGE); Raposo, EP (Raposo, EP); Stanley, HE (Stanley, HE); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICAL REVIEW E Volume: 64 Issue: 4 Article Number: 041108 DOI: 10.1103/PhysRevE.64.041108 Part: Part 1 Published: OCT 2001
Abstract: We consider a Levy flyer of order alpha that starts from a point x(o) on an interval [O,L] with absorbing boundaries. We find a closed-form expression for the average number of flights the flyer takes and the total length of the flights it travels before it is absorbed. These two quantities are equivalent to the mean first passage times for Levy flights and Levy walks, respectively. Using fractional differential equations with a Riesz kernel, we find exact analytical expressions for both quantities in the continuous limit. We show that numerical solutions for the discrete Levy processes converge to the continuous approximations in all cases except the case of alpha–>2, and the cases of x(o)–>0 and x(o)-L. For alpha >2, when the second moment of the flight length distribution exists, our result is replaced by known results of classical diffusion. We show that if x(o) is placed in the vicinity of absorbing boundaries, the average total length has a minimum at alpha =1, corresponding to the Cauchy distribution. We discuss the relevance of this result to the problem of foraging, which has received recent attention in the statistical physics literature.
Title: Levy fights search patterns of biological organisms
Author(s): Viswanathan, GM (Viswanathan, GM); Afanasyev, V (Afanasyev, V); Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); da Luz, MGE (da Luz, MGE); Raposo, EP (Raposo, EP); Stanley, HE (Stanley, HE)
Source: PHYSICA A Volume: 295 Issue: 1-2 Pages: 85-88 DOI: 10.1016/S0378-4371(01)00057-7 Published: JUN 1 2001
Abstract: We discuss recent findings suggesting that an inverse square probability density distribution P(l)similar tol(-2) of step lengths l leads to an optimal random search strategy for organisms that can search efficiently for randomly located objects that can only be detected in the limited vicinity of the searcher and can be revisited any number of times. We explore the extent to which these findings may be dependent on the dimensionality of the search space and the presence of short-range correlations in the step lengths and directions. (C) 2001 Elsevier Science B.V, All rights reserved.
Title: Improvements in the statistical approach to random Levy flight searches
Author(s): da Luz, MGE (da Luz, MGE); Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); Raposo, EP (Raposo, EP); Stanley, HE (Stanley, HE); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A Volume: 295 Issue: 1-2 Pages: 89-92 DOI: 10.1016/S0378-4371(01)00058-9 Published: JUN 1 2001
Abstract: Recently it has been shown that the most efficient strategy for searching randomly located objects, when the sites are randomly distributed and can be revisited any number of times, leads to a power law distribution P(l) = l(-mu) of the flights l, with mu = 2. We show analytically that the incorporation of energy considerations limits the possible range for the Levy exponent mu, however, mu =2 still emerges as the optimal foraging condition. Furthermore, we show that the probability distribution of flight lengths for the short and intermediate flight length regimes depends on the details of the system. (C) 2001 Elsevier Science B.V, All rights reserved.
Title: Statistical physics of random searches
Author(s): Viswanathan, GM (Viswanathan, GM); Afanasyev, V (Afanasyev, V); Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); da Luz, MGE (da Luz, MGE); Raposo, EP (Raposo, EP); Stanley, HE (Stanley, HE)
Source: BRAZILIAN JOURNAL OF PHYSICS Volume: 31 Issue: 1 Pages: 102-108 Published: MAR 2001
Abstract: We apply the theory of random walks to quantitatively describe the general problem of how to search efficiently for randomly located objects that can only be detected in the limited vicinity of a searcher who typically has a finite degree of “free will” to move and search at will. We illustrate Levy flight search processes by comparison to Brownian random walks and discuss experimental observations of Levy flights in the special case of biological organisms that search for food sites. We review recent findings indicating that an inverse square probability density distribution P(l) similar to l(-2) of step lengths l can lead to optimal searches. Finally we survey the explanations put forth to account for these surprising findings.
Author(s): da Silva, RG (da Silva, RG); Lyra, ML (Lyra, ML); da Silva, CR (da Silva, CR); Viswanathan, GM (Viswanathan, GM)
Source: EUROPEAN PHYSICAL JOURNAL B Volume: 17 Issue: 4 Pages: 693-697 DOI: 10.1007/s100510070110 Published: OCT 2000
Abstract: In this work, we introduce a restricted ballistic deposition model with symmetric growth rules that favors the formation of local finite slopes. It is the simplest model which, even without including a diffusive relaxation mode of the interface, leads to a macroscopic groove instability By employing a finite-size scaling of numerical simulation data, we determine the scaling behavior of the surface structure grown over a one-dimensional substrate of linear size L. We found that the surface profile develops a macroscopic groove with the asymptotic surface width scaling as w(sat) proportional to L-alpha, with alpha = 1. The early-time dynamics is governed by the scaling law w proportional to t(beta), with beta = 1/2. We further investigate the sensitivity to initial conditions of the present model by applying damage spreading techniques. We find that the early-time distance between two initially close surface configurations grows in a ballistic fashion as D proportional to t, but a slower Brownian-like scaling (D proportional to t(1/2)) sets up for evolution times much larger than a characteristic time scale t(x) proportional to L-2.
Title: Boundary condition dependence of cluster size ratios in random percolation
Author(s): da Silva, CR (da Silva, CR); Lyra, ML (Lyra, ML); Viswanathan, GM (Viswanathan, GM)
Source: INTERNATIONAL JOURNAL OF MODERN PHYSICS C Volume: 11 Issue: 7 Pages: 1411-1415 DOI: 10.1142/S0129183100001231 Published: OCT 2000
Abstract: We study the ratio of the number of sites in the largest and second largest clusters in random percolation. Using the scaling hypothesis that the ratio [M-1]/[M-2] of the mean cluster sizes M-1 and M-2 scales as f((p – p(c))L-1/nu), we employ finite-size scaling analysis to find that [M-1]/[M-2] is nonuniversal with respect to the boundary conditions imposed. The mean [M-1/M-2] of the ratios behaves similarly although with a distinct critical value reflecting the relevance of mass fluctuations at the percolation threshold. These sere exponent ratios also allow for reliable estimates of the critical parameters at percolation from relatively small lattices.
Title: Efficient search method for obtaining critical properties
Author(s): Fulco, UL (Fulco, UL); Nobre, FD (Nobre, FD); da Silva, LR (da Silva, LR); Lucena, LS (Lucena, LS); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A Volume: 284 Issue: 1-4 Pages: 223-230 DOI: 10.1016/S0378-4371(00)00217-X Published: SEP 1 2000
Abstract: A method for obtaining critical properties is presented. Based on self-organized criticality, it drives the system spontaneously to the critical point, providing an efficient way to estimate critical properties. The method is illustrated for Ising spin systems, and despite the small lattice sizes used, it yields critical temperatures and beta exponents in good agreement with those available in the literature. (C) 2000 Elsevier Science B.V. All rights reserved.
Author(s): Viswanathan, GM (Viswanathan, GM); Buldyrev, SV (Buldyrev, SV); Garger, EK (Garger, EK); Kashpur, VA (Kashpur, VA); Lucena, LS (Lucena, LS); Shlyakhter, A (Shlyakhter, A); Stanley, HE (Stanley, HE); Tschiersch, J (Tschiersch, J)
Source: PHYSICAL REVIEW E Volume: 62 Issue: 3 Pages: 4389-4392 DOI: 10.1103/PhysRevE.62.4389 Part: Part b Published: SEP 2000
Abstract: We analyze nonstationary Cs-137 atmospheric activity concentration fluctuations measured near Chernobyl after the 1986 disaster and find three new results: (i) the histogram of fluctuations is well described by a log-normal distribution; (ii) there is a pronounced spectral component with period T=1 yr, and (iii) the fluctuations are long-range correlated. These findings allow us to quantify two fundamental statistical properties of the data: the probability distribution and the correlation properties of the time series. We interpret our findings as evidence that the atmospheric radionuclide resuspension processes are tightly coupled to the surrounding ecosystems and to large time scale weather patterns.
Title: Levy flights in random searches
Author(s): Viswanathan, GM (Viswanathan, GM); Afanasyev, V (Afanasyev, V); Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); da Luz, MGE (da Luz, MGE); Raposo, EP (Raposo, EP); Stanley, HE (Stanley, HE)
Source: PHYSICA A Volume: 282 Issue: 1-2 Pages: 1-12 DOI: 10.1016/S0378-4371(00)00071-6 Published: JUL 1 2000
Abstract: We review the general search problem of how to find randomly located objects that can only be detected in the limited vicinity of a forager, and discuss its quantitative description using the theory of random walks. We illustrate Levy flight foraging by comparison to Brownian random walks and discuss experimental observations of Levy flights in biological foraging. We review recent findings suggesting that an inverse square probability density distribution P(l) similar to l(-2) Of step lengths l can lead to optimal searches. Finally, we survey the explanations put forth to account for these unexpected findings. (C) 2000 Published by Elsevier Science B.V. All rights reserved.
Title: A new model to simulate the growth of branched polymers
[I have tried but failed to obtain this article. I’d like a copy of this paper if you have it. -Gandhi]
Author(s): Rego, H (Rego, H); Lucena, L (Lucena, L); Viswanathan, GM (Viswanathan, GM)
Editor(s): Landau DP; Lewis SP; Schuttler HB
Source: COMPUTER SIMULATION STUDIES IN CONDENSED-MATTER PHYSICS XIIBook Series: SPRINGER PROCEEDINGS IN PHYSICS Volume: 85 Pages: 223-227 Published: 2000
Abstract: We propose a model to simulate branched polymers in disordered media, based on a model introduced by Lucena et al. [Phys. Rev. Lett. 72, 230 (1994)] In this new model we maintain the number of active tips fixed in the time, instead of growing as a power-law like in the original model. We compare Our results with another growth mechanism based on the self-organized criticality (SOC) concept.
Title: Optimizing the success of random searches
Author(s): Viswanathan, GM (Viswanathan, GM); Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); da Luz, MGE (da Luz, MGE); Raposo, EP (Raposo, EP); Stanley, HE (Stanley, HE)
Source: NATURE Volume: 401 Issue: 6756 Pages: 911-914 DOI: 10.1038/44831 Published: OCT 28 1999
Abstract: We address the general question of what is the best statistical strategy to adapt in order to search efficiently for randomly located objects (‘target sites’). It is often assumed in foraging theory that the flight lengths of a forager have a characteristic scale: from this assumption gaussian, Rayleigh and other classical distributions with well-defined variances have arisen. However, such theories cannot explain the long-tailed power-law distributions(1,2) of flight lengths or flight times(3-6) that are observed experimentally. Here we study how the search efficiency depends on the probability distribution of flight lengths taken by a forager that can detect target sites only in its limited vicinity. We show that, when the target sites are sparse and can be visited any number of times, an inverse square power-law distribution of flight lengths, corresponding to Levy flight motion, is an optimal strategy. We test the theory by analysing experimental foraging data on selected insect, mammal and bird species, and find that they are consistent with the predicted inverse square power-law distributions.
Title: Efficient search of critical points in Ising-like systems
Author(s): Fulco, UL (Fulco, UL); Lucena, LS (Lucena, LS); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A Volume: 264 Issue: 1-2 Pages: 171-179 DOI: 10.1016/S0378-4371(98)00469-5 Published: FEB 15 1999
Abstract: We propose a simulation method inspired by self-organization that drives Ising-like magnetic systems rapidly to criticality. We develop a feedback control rule with very few parameters for use with the standard methods of local spin updatings that spontaneously leads the system to the critical temperature. This method for predicting the critical values requires small lattices. It gives good results eg., 1% accuracy for T-C in 3-D for 10(3) systems, with reduced computer times, for both Glauber and Metropolis dynamics. (C) 1999 Elsevier Science B.V. All rights reserved.
Title: Scale-invariant correlations in the biological and social sciences
Author(s): Stanley, HE (Stanley, HE); Amaral, LAN (Amaral, LAN); Andrade, JS (Andrade, JS); Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); Makse, HA (Makse, HA); Peng, CK (Peng, CK); Suki, B (Suki, B); Viswanathan, G (Viswanathan, G)
Source: PHILOSOPHICAL MAGAZINE B-PHYSICS OF CONDENSED MATTER STATISTICAL MECHANICS ELECTRONIC OPTICAL AND MAGNETIC PROPERTIES Volume: 77 Issue: 5 Pages: 1373-1388 DOI: 10.1080/13642819808205030 Published: MAY 1998
Abstract: In this opening introductory paper, we discuss the possibility that scale-invariant correlations may be a feature of biological and possibly even social systems. We illustrate this possibility by reviewing recent work at Boston University. Specifically, we focus first on the apparent scale-invariant correlations in non-coding deoxyribonucleic acid (DNA) and show that this feature can be used to distinguish coding and non-coding DNA. We argue that the inflating a degassed lung is characterized by a cascade of avalanches, as the airways successively open, and that distribution functions characterizing this cascade are scale invariant. Moving from the lung to the heart, we find that the sequence of interbeat intervals is characterized by scale-invariant correlations in health, but not in disease. Moving from individual organs to entire organisms, we discuss recent experimental evidence that the foraging behaviour of the wandering albatross is governed by a scale-invariant Levy distribution. Finally, we enquire whether scale invariance describes not only animal behaviour but also human behaviour. To this end, we analyse data on urban growth patterns, on finance and on economics. For all cases, we find empirical evidence of scaling behaviour. We conclude by asking why such complex systems might display scale invariance.
Title: Analysis of DNA sequences using methods of statistical physics
Author(s): Buldyrev, SV (Buldyrev, SV); Dokholyan, NV (Dokholyan, NV); Goldberger, AL (Goldberger, AL); Havlin, S (Havlin, S); Peng, CK (Peng, CK); Stanley, HE (Stanley, HE); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A Volume: 249 Issue: 1-4 Pages: 430-438 DOI: 10.1016/S0378-4371(97)00503-7 Published: FEB 1 1998
Abstract: We review the present status of the studies of DNA sequences using methods of statistical physics. We present evidence, based on systematic studies of the entire GenBank database, supporting the idea that the DNA sequence in genes containing noncoding regions is correlated, and that the correlation is remarkably long range, i.e., base pails thousands of base pairs distant are correlated. We do not find such a long-range correlation in the coding regions of the DNA. We discuss the mechanisms of molecular evution that may lead to the presence of long-range power-law correlations in noncoding DNA and their absence in coding DNA. One such mechanism is the simple repeat expansion, which recently has attracted the attention of the biological community in conjunction with genetic diseases. We also review new tools – e.g., detrended fluctuation analysis – that are useful for studies of complex hierarchical DNA structure. (C) 1998 Elsevier Science B.V. All rights reserved.
Author(s): Viswanathan, GM (Viswanathan, GM); Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); Stanley, HE (Stanley, HE)
Source: PHYSICA A Volume: 249 Issue: 1-4 Pages: 581-586 DOI: 10.1016/S0378-4371(97)00519-0 Published: FEB 1 1998
Abstract: We introduce and develop new techniques to quantify DNA patchiness, and characteristics of their mosaic structure. These techniques, which involve calculating two functions, alpha(l) and beta(l), measure correlation exponents at length scale l and detect distinct characteristic patch sizes embedded in scale invariant patch size distributions. Using these methods, it is possible to address a number of issues relating to the mosaic structure of genomic DNA. We find several distinct characteristic patch sizes in yeast, human, and prokaryotic sequences. We also find that the distinct patch sizes in all 16 yeast chromosomes are similar. (C) 1998 Published by Elsevier Science B.V. All rights reserved.
Title: Quantification of DNA patchiness using long-range correlation measures (vol 72, pg 866, 1997)
Author(s): Viswanathan, GM (Viswanathan, GM); Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); Stanley, HE (Stanley, HE)
Source: BIOPHYSICAL JOURNAL Volume: 73 Issue: 5 Pages: 2848-2849 Published: NOV 1997
Title: Quantification of DNA patchiness using long-range correlation measures
Author(s): Viswanathan, GM (Viswanathan, GM); Buldyrev, SV (Buldyrev, SV); Havlin, S (Havlin, S); Stanley, HE (Stanley, HE)
Source: BIOPHYSICAL JOURNAL Volume: 72 Issue: 2 Pages: 866-875 Part: Part 1 Published: FEB 1997
Abstract: We introduce and develop new techniques to quantify DNA patchiness, and to quantify characteristics of its mosaic structure. These techniques, which involve calculating two functions, alpha(l) and beta(l), measure correlations at length scale a and detect distinct characteristic patch sizes embedded in scale-invariant patch size distributions. Using these new methods, we address a number of issues relating to the mosaic structure of genomic DNA. We find several distinct characteristic patch sizes in certain genomic sequences, and compare, contrast, and quantify the correlation properties of different sequences, including a number of yeast, human, and prokaryotic sequences. We exclude the possibility that the correlation properties and the known mosaic structure of DNA can be explained either by simple Markov processes or by tandem repeats of dinucleotides. We find that the distinct patch sizes in all 16 yeast chromosomes are similar. Furthermore, we test the hypothesis that, for yeast, patchiness is caused by the alternation of coding and noncoding regions, and the hypothesis that in human sequences patchiness is related to repetitive sequences. We find that, by themselves, neither the alternation of coding and noncoding regions, nor repetitive sequences, can fully explain the long-range correlation properties of DNA.
Title: Deviations from uniform power law scaling in nonstationary time series
Author(s): Viswanathan, GM (Viswanathan, GM); Peng, CK (Peng, CK); Stanley, HE (Stanley, HE); Goldberger, AL (Goldberger, AL)
Source: PHYSICAL REVIEW E Volume: 55 Issue: 1 Pages: 845-849 DOI: 10.1103/PhysRevE.55.845 Part: Part b Published: JAN 1997
Abstract: A classic problem in physics is the analysis of highly nonstationary time series that typically exhibit long-range correlations. Here we test the hypothesis that the scaling properties of the dynamics of healthy physiological systems are more stable than those of pathological systems by studying beat-to-beat fluctuations in the human heart rate. We develop techniques based on the Fano factor and Allan factor functions, as well as on detrended fluctuation analysis, for quantifying deviations from uniform power-law scaling in nonstationary time series. By analyzing extremely long data sets of up to N = 10(5) beats for 11 healthy subjects, we find that the fluctuations in the heart rate scale approximately uniformly over several temporal orders of magnitude. By contrast, we find that in data sets of comparable length for 14 subjects with heart disease, the fluctuations grow erratically, indicating a loss of scaling stability.
Title: Scaling properties of DNA sequences and heartbeat rate
Author(s): Havlin, S (Havlin, S); Buldyrev, SV (Buldyrev, SV); Ivanov, PC (Ivanov, PC); Rosenblum, MG (Rosenblum, MG); Stanley, HE (Stanley, HE); Viswanathan, GM (Viswanathan, GM); Peng, CK (Peng, CK); Goldberger, AL (Goldberger, AL)
Editor(s): Mallamace F; Stanley HE
Source: PHYSICS OF COMPLEX SYSTEMSBook Series: PROCEEDINGS OF THE INTERNATIONAL SCHOOL OF PHYSICS ENRICO FERMI Volume: 134 Pages: 445-472 Published: 1997
Title: Scaling and universality in animate and inanimate systems
Author(s): Stanley, HE (Stanley, HE); Amaral, LAN (Amaral, LAN); Buldyrev, SV (Buldyrev, SV); Goldberger, AL (Goldberger, AL); Havlin, S (Havlin, S); Leschhorn, H (Leschhorn, H); Maass, P (Maass, P); Makse, HA (Makse, HA); Peng, CK (Peng, CK); Salinger, MA (Salinger, MA); Stanley, MHR (Stanley, MHR); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A Volume: 231 Issue: 1-3 Pages: 20-48 DOI: 10.1016/0378-4371(96)00086-6 Published: SEP 15 1996
Abstract: We illustrate the general principle that in biophysics, econophysics and possibly even city growth, the conceptual framework provided by scaling and universality may be of use in making sense of complex statistical data. Specifically, we discuss recent work on DNA sequences, heartbeat intervals, avalanche-like lung inflation, urban growth, and company growth. Although our main focus is on data, we also discuss statistical mechanical models.
Title: Scaling and universality in living systems
Author(s): Stanley, HE (Stanley, HE); Amaral, LAN (Amaral, LAN); Buldyrev, SV (Buldyrev, SV); Goldberger, AL (Goldberger, AL); Havlin, S (Havlin, S); Hyman, BT (Hyman, BT); Leschhorn, H (Leschhorn, H); Maass, P (Maass, P); Makse, HA (Makse, HA); Peng, CK (Peng, CK); Salinger, MA (Salinger, MA); Stanley, MHR (Stanley, MHR); Viswanathan, GM (Viswanathan, GM)
Source: FRACTALS-AN INTERDISCIPLINARY JOURNAL ON THE COMPLEX GEOMETRY OF NATURE Volume: 4 Issue: 3 Pages: 427-451 DOI: 10.1142/S0218348X96000558 Published: SEP 1996
Title: Levy flight search patterns of wandering albatrosses
Author(s): Viswanathan, GM (Viswanathan, GM); Afanasyev, V (Afanasyev, V); Buldyrev, SV (Buldyrev, SV); Murphy, EJ (Murphy, EJ); Prince, PA (Prince, PA); Stanley, HE (Stanley, HE)
Source: NATURE Volume: 381 Issue: 6581 Pages: 413-415 DOI: 10.1038/381413a0 Published: MAY 30 1996
Abstract: LEVY flights are a special class of random walks whose step lengths are not constant but rather are chosen from a probability distribution with a power-law tail. Realizations of Levy flights in physical phenomena are very diverse, examples including fluid dynamics, dynamical systems, and micelles(1,2). This diversity raises the possibility that Levy flights may be found in biological systems. A decade ago, it was proposed that Levy flights may be observed in the behaviour of foraging ants(3). Recently, it was argued that Drosophila might perform Levy flights(4), but the hypothesis that foraging animals in natural environments perform Levy flights has not been tested, Here we study the foraging behaviour of the wandering albatross Diomedea exulans, and find a power-law distribution of flight-time intervals. We interpret our finding of temporal scale invariance in terms of a scale-invariant spatial distribution of food on the ocean surface. Finally, we examine the significance of our finding in relation to the basis of scale-invariant phenomena observed in biological systems.
Title: Anomalous fluctuations in the dynamics of complex systems: From DNA and physiology to econophysics
Author(s): Stanley, HE (Stanley, HE); Afanasyev, V (Afanasyev, V); Amaral, LAN (Amaral, LAN); Buldyrev, SV (Buldyrev, SV); Goldberger, AL (Goldberger, AL); Havlin, S (Havlin, S); Leschhorn, H (Leschhorn, H); Maass, P (Maass, P); Mantegna, RN (Mantegna, RN); Peng, CK (Peng, CK); Prince, PA (Prince, PA); Salinger, MA (Salinger, MA); Stanley, MHR (Stanley, MHR); Viswanathan, GM (Viswanathan, GM)
Source: PHYSICA A-STATISTICAL MECHANICS AND ITS APPLICATIONS Volume: 224 Issue: 1-2 Pages: 302-321 DOI: 10.1016/0378-4371(95)00409-2 Published: FEB 1 1996
Abstract: We discuss examples of complex systems composed of many interacting subsystems. We focus on those systems displaying nontrivial long-range correlations. These include the one-dimensional sequence of base pairs in DNA, the sequence of flight times of the large seabird Wandering Albatross, and the annual fluctuations in the growth rate of business firms. We review formal analogies in the models that describe the observed long-range correlations, and conclude by discussing the possibility that behavior of large numbers of humans (as measured, e.g., by economic indices) might conform to analogs of the scaling laws that have proved useful in describing systems composed of large numbers of inanimate objects.
END
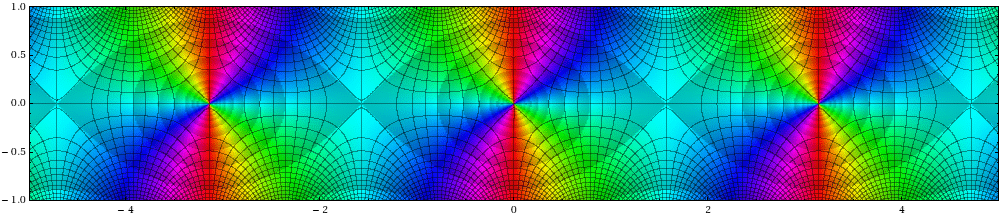
Pingback: List of publications | Gandhi Viswanathan's Blog